grama package¶
Subpackages¶
- grama.data package
- grama.dfply package
- Submodules
- grama.dfply.base module
- grama.dfply.count module
- grama.dfply.group module
- grama.dfply.join module
- grama.dfply.mask_helpers module
- grama.dfply.reshape module
- grama.dfply.select module
- grama.dfply.set_ops module
- grama.dfply.string_helpers module
- grama.dfply.subset module
- grama.dfply.summarize module
- grama.dfply.summary_functions module
- grama.dfply.transform module
- grama.dfply.vector module
- grama.dfply.window_functions module
- Module contents
- grama.eval package
- grama.fit package
- grama.models package
- Submodules
- grama.models.cantilever_beam module
- grama.models.channel1d module
- grama.models.circuit_RLC module
- grama.models.ishigami module
- grama.models.linear_normal module
- grama.models.pareto_random module
- grama.models.plane_laminate module
- grama.models.plate_buckling module
- grama.models.poly module
- grama.models.test module
- grama.models.time_cantilever module
- grama.models.trajectory_linear_drag module
- Module contents
- grama.tran package
Submodules¶
grama.comp_building module¶
-
grama.comp_building.comp_freeze¶ Freeze inputs to a model
Composition. Remove inputs from a model by “freezing” them to fixed values.
Parameters: - model (gr.Model) – Model to compose
- df (pd.DataFrame) – DataFrame of values for freeze
- var (dict) – Dictionary of inputs to freeze (keys) to specific values (value) Provide each key/value pair as a keyword argument
Returns: New model with frozen inputs
Return type: gr.Model
- Examples::
- import grama as gr
-
grama.comp_building.comp_function¶ Add a function to a model
Composition. Add a (non-vectorized) function to an existing model. See
gr.comp_vec_function()to add a function that is vectorized over DataFrames.Parameters: - model (gr.Model) – Model to compose
- fun (function) – Function taking at least one real input and returns at least one real output (fun: R^d -> R^r). Each input to fun must be a scalar (See examples below).
- var (list(string)) – List of variable names or number of inputs
- out (list(string)) – List of output names or number of outputs
- runtime (numeric) – Estimated single-eval runtime (in seconds)
Returns: New model with added function
Return type: gr.Model
@pre (len(var) == d) | (var == d) @pre (len(out) == r) | (var == r)
Examples:
import grama as gr ## Simple example md = ( gr.Model("test") >> gr.cp_function( fun=lambda x: x, var=["x"], out=["y"], name="identity" ) ) ## Providing a function with multiple inputs md2 = ( gr.Model("test 2") >> gr.cp_function( fun=lambda x, y: x + y, var=["x", "y"], out=["f"], ) ) ## Providing a function with multiple inputs and multiple outputs md3 = ( gr.Model("test 3") >> gr.cp_function( fun=lambda x, y: [x + y, x - y], var=["x", "y"], out=["f", "g"], ) )
-
grama.comp_building.comp_vec_function¶ Add a vectorized function to a model
Composition. Add a function to an existing model. Function must be vectorized over DataFrames, and must add new columns matching its out set. See
gr.cp_function()to add a non-vectorized function.Notes
The helper function
gr.df_make()is useful for constructing a vectorized lambda function (see Examples below).Parameters: - model (gr.model) – Model to compose
- fun (function) – Function taking R^d -> R^r; must be vectorized over DataFrames; it must take a DataFrame as input and return a new DataFrame
- var (list(string)) – List of variable names or number of inputs
- out (list(string)) – List of output names or number of outputs
- runtime (numeric) – Estimated single-eval runtime (in seconds)
Returns: New model with added function
Return type: gr.model
@pre (len(var) == d) | (var == d) @pre (len(out) == r) | (var == r)
Examples:
import grama as gr ## Simple example md = ( gr.Model("Test") >> gr.cp_vec_function( fun=lambda df: gr.df_make(y=1 + 0.5 * df.x), var=["x"], out=["y"], name="Simple linear function", ) )
-
grama.comp_building.comp_md_det¶ Add a Model with deterministic evaluation
Composition. Add a model as function to an existing model. Evaluate the model deterministically (ignore any random variables).
Parameters: - model (gr.model) – Model to compose
- md (gr.model) – Model to add as function
Returns: New model with added function
Return type: gr.model
Examples:
import grama as gr from grama.models import make_cantilever_beam ## Use functions from beam model, but introduce new marginals md_plate = ( gr.Model("New beam model") >> gr.cp_md_det(md=make_cantilever_beam()) >> gr.cp_marginals( H=gr.marg_mom("norm", mean=1000, cov=0.1), V=gr.marg_mom("norm", mean=500, cov=0.1), ) >> gr.cp_copula_independence() )
-
grama.comp_building.comp_md_sample¶ Add a Model with sampled evaluation
Composition. Add a model as function to an existing model. Evaluate the model via sampling (one sample per evaluation). Use param to turn model parameters into variables of new model. Random variables of composed model are turned into outputs of new model.
Parameters: - model (gr.model) – Model to compose
- md (gr.model) – Model to add as function
- param (dict) – Parameters in md to treat as var; entries must be of the form “var”: (“param1”, “param2”, …)
- rand2out (bool) – Add model’s var_rand to outputs (to track values)
Returns: New model with added function
Return type: gr.model
Examples:
-
grama.comp_building.comp_bounds¶ Add variable bounds to a model
Composition. Add variable bounds to an existing model. Bounds are specified by iterable; the model variable name is specified by the keyword argument name.
Parameters: model (gr.model) – Model to modify - Kwargs:
- var (iterable): Bound information; keyword argument name is targeted variable, value should be a length 2 iterable of the form (lower_bound, upper_bound)
Returns: Model with new marginals Return type: gr.model @pre len(var) >= 2
Examples:
import grama as gr md = ( gr.Model("Simple Model") >> gr.cp_function( lambda x: x[0] + x[1], var=["x0", "x1"], out=1 ) >> gr.cp_bounds( x0=(-1, 1), # Finite bounds x1=(0, np.inf) # Semi-infinite bounds ) )
-
grama.comp_building.comp_copula_independence¶ Add an independence copula to model
Composition. Add an independence copula to an existing model.
NOTE: Independence of random variables is a very strong assumption! Recommend using comp_copula_gaussian instead.
Parameters: model (gr.model) – Model to modify Returns: Model with independence copula Return type: gr.model Examples:
import grama as gr md = ( gr.Model() >> gr.cp_marginals( x0=gr.marg_mom("norm", mean=0, sd=1), x1=gr.marg_mom("beta", mean=0, sd=1, skew=0, kurt=2), ) >> gr.cp_copula_independence() )
-
grama.comp_building.comp_copula_gaussian¶ Add a Gaussian copula to model
Composition. Add a gaussian copula to an existing model.
Parameters: - model (gr.model) – Model to modify
- df_corr (DataFrame) – Correlation information
- df_data (DataFrame) – Data for automated fitting
Returns: Model with Gaussian copula
Return type: gr.model
Examples:
import grama as gr ## Manual assignment md_manual = (gr.Model() >> gr.cp_marginals( x0=gr.marg_mom("norm", mean=0, sd=1), x1=gr.marg_mom("uniform", mean=0, sd=1), ) >> gr.cp_copula_gaussian( # Specify correlation structure explicitly df_corr=gr.df_make(var1="x0", var2="x1", corr=0.5) ) ) ## Automated fitting from grama.data import df_stang md_auto = ( gr.Model() >> gr.cp_marginals( E=gr.marg_fit("norm", df_stang.E), mu=gr.marg_fit("beta", df_stang.mu), thick=gr.marg_fit("norm", df_stang.thick) ) >> gr.cp_copula_gaussian(df_data=df_stang) )
-
grama.comp_building.comp_marginals¶ Add marginals to a model
Composition. Add marginals to an existing model. Marginals are specified either by dictionary entries or by gr.Marginal() object. The model variable name is specified by the keyword argument name.
Notes
Several helper functions are available to fit marginal distributions
gr.marg_fit()fits a distribution using a dataset (via maximum likelihood estimation)gr.marg_mom()fits a distribution using moments (via the method of moments)gr.marg_gkde()fits a gaussian kernel density using a dataset
Parameters: - model (gr.model) – Model to modify
- var (dict OR gr.Marginal) – Marginal information
Returns: Model with new marginals
Return type: gr.model
Examples:
import grama as gr ## Print all of the grama-supported distributions print(gr.valid_dist.keys()) ## Construct a simple example model md = ( gr.Model() >> gr.cp_function( lambda x: x[0] + x[1], var=["x0", "x1"], out=["y"], ) >> gr.cp_marginals( x0=gr.marg_mom("norm", mean=0, sd=1), ) )
-
grama.comp_building.getvars(f)¶ Get a function’s variable names
Convenience function for extracting a function’s variable names. Intended for use with gr.cp_function().
Parameters: f (function) – Function whose variable names are desired Returns: Variable names Return type: tuple - Examples::
import grama as gr
- def fun(x, y, z):
- return x + y + z
- md = (
gr.Model(“Test model”) >> gr.cp_function(
fun=fun, var=gr.getvars(fun), out=[“w”],)
)
grama.comp_metamodels module¶
-
grama.comp_metamodels.comp_metamodel¶ Create a metamodel
Composition: Create a metamodel from an existing model. This convenience function essentially applies a recipe of Evaluation followed by Fitting. Default methods are Latin Hypercube Evaluation and Ordinary Least Squares Fitting with linear features.
Parameters: Returns: Metamodel
Return type: gr.model
grama.core module¶
-
class
grama.core.CopulaIndependence(var_rand)¶ Bases:
grama.core.Copula-
copy()¶ Copy
Returns: Copy of present copula Return type: gr.CopulaIndependence
-
d(u)¶ Density function
Parameters: u (array-like) – Returns: Copula density values Return type: array
-
dudz(z)¶ Jacobian
Parameters: z (array-like) – Returns: Return type: array
-
sample(n=1, seed=None)¶ Draw samples from copula
Parameters: - n (int) – Number of samples
- seed (int) – Random seed
Returns: Independent samples
Return type: DataFrame
-
summary()¶
-
u2z(u)¶ Transform to standard-normal space
Parameters: u (array-like) – Returns: Return type: array
-
z2u(z)¶ Transform to uniform-marginal space
Parameters: z (array-like) – Returns: Return type: array
-
-
class
grama.core.CopulaGaussian(var_rand, df_corr)¶ Bases:
grama.core.Copula-
copy()¶ Copy
Parameters: self (gr.CopulaGaussian) – Returns: Return type: gr.CopulaGaussian
-
d(u)¶ Copula density function
Parameters: u (array-like) – Returns: Return type: array
-
dudz(z)¶ Jacobian
Parameters: z (array-like) – Returns: Return type: array
-
sample(n=1, seed=None)¶ Draw samples from copula
Draw samples according to gaussian copula dependence structure.
Parameters: - self (gr.CopulaGaussian) –
- n (int) – Number of samples to draw
Returns: Copula samples
Return type: array
-
summary()¶
-
u2z(u)¶ Transform to standard-normal space
Parameters: u (array-like) – Returns: Return type: array
-
z2u(z)¶ Transform to uniform-marginal space
Parameters: z (array-like) – Returns: Return type: array
-
-
class
grama.core.Domain(bounds=None, feasible=None)¶ Bases:
objectParent class for input domains
The domain defines constraints on the variables. Together with a model’s functions, it defines the mathematical domain of a model.
-
bound_summary(var)¶
-
copy()¶
-
get_bound(var)¶
-
get_nominal(var)¶
-
get_width(var)¶
-
update()¶
-
-
class
grama.core.Density(marginals=None, copula=None)¶ Bases:
objectParent class for joint densities
The density is defined for all the random variables; therefore it explicitly defines the list of random variables, and together implicitly defines the deterministic variables via
domain.var + [functions.var] - density.marginals.keys()-
copy()¶
-
d(df)¶ Evaluate PDF
Evaluate the PDF of the density.
Parameters: df (DataFrame) – Values
-
pr2sample(df_prval)¶ Convert CDF probabilities to samples
Convert random variable CDF probabilities to random variable samples. Ignores dependence structure.
Parameters: df_prval (DataFrame) – Values in [0,1] Returns: Variable samples (quantiles) Return type: DataFrame @pre df_prval.shape[1] == len(self.var_rand) @post result.shape[1] == len(self.var_rand)
-
sample(n=1, seed=None)¶ Draw samples from joint density
Draw samples according to joint density using marginal and copula information.
Parameters: - n (int) – Number of samples to draw
- seed (int) – random seed to use
Returns: Joint density samples
Return type: DataFrame
-
sample2pr(df_sample)¶ Convert samples to CDF probabilities
Convert random variable samples to CDF probabilities. Ignores dependence structure.
Parameters: df_sample (DataFrame) – Values in [0,1] Returns: Variable samples (quantiles) Return type: DataFrame @pre df_sample.shape[1] == len(self.var_rand) @post result.shape[1] == len(self.var_rand)
-
summary_copula()¶
-
summary_marginal(var)¶
-
-
class
grama.core.Function(func, var, out, name, runtime)¶ Bases:
objectParent class for functions.
A function specifies its own inputs and outputs; these are subsets of the full model’s inputs and outputs.
-
copy()¶ Make a copy
-
eval(df)¶ Evaluate function
Evaluate a grama function; loops over dataframe rows. Intended for internal use.
Args: df (DataFrame): Input values to evaluate
Returns: Result values Return type: DataFrame
-
summary()¶ Returns a summary string
-
-
class
grama.core.FunctionModel(md, ev=None, var=None, out=None)¶ Bases:
grama.core.Functiongr.Model as gr.Function
-
copy()¶ Make a copy
-
eval(df)¶ Evaluate function; DataFrame vectorized
Evaluate grama model as a function. Modify the parameters before
Parameters: df (DataFrame) – Input values to evaluate Returns: Result values Return type: DataFrame
-
-
class
grama.core.FunctionVectorized(func, var, out, name, runtime)¶ Bases:
grama.core.Function-
copy()¶ Make a copy
-
eval(df)¶ Evaluate function; DataFrame vectorized
Evaluate grama function. Assumes function is vectorized over dataframes.
Parameters: df (DataFrame) – Input values to evaluate Returns: Result values Return type: DataFrame
-
-
class
grama.core.Model(name=None, functions=None, domain=None, density=None)¶ Bases:
objectParent class for grama models.
-
copy()¶ Make a copy of this model
-
det_nom()¶ Return nominal conditions for deterministic variables
Returns: Nominal values for deterministic variables Return type: DataFrame
-
dxdz(z)¶ Inverse transform jacobian
Compute jacobian of the inverse transform X = phi^{-1}(Z)
Parameters: z (array) – Single vector of standard normal values. Order of entries must match self.var_rand Returns: Jacobian of inverse transform Return type: 2d array
-
evaluate_df(df)¶ Evaluate function using an input dataframe
Parameters: df (DataFrame) – Variable values at which to evaluate model functions Returns: Output results Return type: DataFrame
-
make_dag(expand={})¶ Generate a DAG for the model
-
name_corr()¶ Name the correlation elements
-
norm2rand(df)¶ Transform standard normal samples to model random variable space
Transform a DataFrame of standard normal samples to model random variable space.
Parameters: df (DataFrame) – Random variable samples; must have columns for all of self.var_rand. Returns: Samples in standard-normal space Return type: DataFrame
-
printpretty()¶ Formatted print of model attributes
-
rand2norm(df)¶ Transform random samples to standard normal space
Transform a DataFrame of random variable samples to standard normal space
Parameters: df (DataFrame) – Random variable samples; must have columns for all of self.var_rand. Returns: Samples in standard-normal space Return type: DataFrame
-
runtime(n)¶ Estimate runtime
Estimate the total runtime to evaluate n observations.
Parameters: - self (gr.Model) –
- n (int) – Number of observations
Returns: Estimated runtime, in seconds
Return type: float
-
runtime_message(df)¶ Runtime message
Estimate total runtime based on proposed DataFrame, prepare a message for console print.
Parameters: - self (gr.Model) –
- df (DataFrame) – Data to evaluate
Returns: Runtime message
Return type: str
-
show_dag(expand={})¶ Generate and show a DAG for the model
-
string_rep()¶
-
update()¶ Update model public attributes based on functions, domain, and density.
The variables and parameters are implicitly defined by the model attributes. For internal use.
- self.functions defines the full list of inputs
- self.domain defines the constraints on the model’s domain
- self.density defines the random variables
-
var_outer(df_rand, df_det=None)¶ Outer product of random and deterministic samples
Parameters: - df_rand (DataFrame) –
- df_det (DataFrame) – set to “nom” for nominal evaluation
Returns: Outer product of samples
Return type: DataFrame
-
x2z(x)¶ Transform to standard normal space
Transform a single vector of random variable values to standard normal space.
Parameters: x (array) – Single vector of values in var_rand. Order of entries must match self.var_rand Returns: Single vector of values transformed to standard normal space Return type: array
-
z2x(z)¶ Transform to random variable space
Transform a single vector of normal values to the model’s random variable space.
Parameters: z (array) – Single vector of standard normal values. Order of entries must match self.var_rand Returns: Single vector of values transformed to model random variable space Return type: array
-
grama.dataframe module¶
-
grama.dataframe.df_equal(df1, df2, close=False, precision=3)¶ Check DataFrame equality
Check that two dataframes have the same columns and values. Allows column order to differ.
Parameters: - df1 (DataFrame) – Comparison input 1
- df2 (DataFrame) – Comparison input 2
Returns: Result of comparison
Return type: bool
-
grama.dataframe.df_make(**kwargs)¶ Construct a DataFrame
Helper function to construct a DataFrame. A common use-case is to use df_make() to pass values to the df (and related) keyword arguments succinctly.
- Kwargs:
- varname (iterable): Column for constructed dataframe; column name inferred from variable name.
Returns: Constructed DataFrame Return type: DataFrame - Preconditions:
- All provided iterables must have identical length or be of length one. All provided variable names (keyword arguments) must be distinct.
Examples:
import grama as gr from models import make_test md = make_test() ( md >> gr.ev_sample( n=1e3, df_det=gr.df_make(x2=[1, 2]) ) )
-
grama.dataframe.df_grid(**kwargs)¶ Construct a DataFrame as outer-product
Helper function to construct a DataFrame as an outer-product of the given columns.
- Kwargs:
- varname (iterable): Column for constructed dataframe; column name inferred from variable name.
Returns: Constructed DataFrame Return type: DataFrame - Preconditions:
- All provided variable names (keyword arguments) must be distinct.
Examples:
import grama as gr ## Make an empty DataFrame gr.df_grid() ## Create a row for every pair of values (6 rows total) gr.df_grid(x=["A", "B"], y=[1, 2, 3])
grama.eval_contour module¶
-
grama.eval_contour.eval_contour¶ Generate contours from a model
Generates contours from a model. Evaluates the model on a dense grid, then runs marching squares to generate contours. Supports targeting multiple outputs and handling auxiliary inputs not included in the contour map.
Parameters: - model (gr.Model) – Model to evaluate.
- var (list of str) – Model inputs to target; must provide exactly two inputs, and both must have finite domain width.
- out (list of str) – Model output(s) for contour generation.
- df (DataFrame or None) – Levels for model variables not included in var (auxiliary inputs). If provided var and model.var contain the same values, then df may equal None.
- levels (dict) – Specific output levels for contour generation; overrides n_levels.
- n_side (int) – Side resolution for grid; n_side**2 total evaluations.
- n_levels (int) – Number of contour levels.
Returns: Points along contours, organized by output and auxiliary variable levels.
Return type: DataFrame
Examples:
import grama as gr ## Multiple outputs ( gr.Model() >> gr.cp_vec_function( fun=lambda df: gr.df_make( f=df.x**2 + df.y**2, g=df.x + df.y, ), var=["x", "y"], out=["f", "g"], ) >> gr.cp_bounds( x=(-1, +1), y=(-1, +1), ) >> gr.ev_contour( var=["x", "y"], out=["f", "g"], ) # Contours with no auxiliary variables can autoplot >> gr.pt_auto() ) ## Auxiliary inputs ( gr.Model() >> gr.cp_vec_function( fun=lambda df: gr.df_make( f=df.c * df.x + (1 - df.c) * df.y, ), var=["x", "y"], out=["f", "g"], ) >> gr.cp_bounds( x=(-1, +1), y=(-1, +1), ) >> gr.ev_contour( var=["x", "y"], out=["f"], df=gr.df_make(c=[0, 1]) ) # Contours with auxiliary variables should be manually plotted >> gr.ggplot(gr.aes("x", "y")) + gr.geom_segment(gr.aes(xend="x_end", yend="y_end", group="level", color="c")) )
grama.eval_defaults module¶
-
grama.eval_defaults.eval_df¶ Evaluate model at given values
Evaluates a given model at a given dataframe.
Parameters: - model (gr.Model) – Model to evaluate
- df (DataFrame) – Input dataframe to evaluate
- append (bool) – Append results to original dataframe?
Returns: Results of model evaluation
Return type: DataFrame
Examples:
import grama as gr from grama.models import make_test md = make_test() df = gr.df_make(x0=0, x1=1, x2=2) md >> gr.ev_df(df=df)
-
grama.eval_defaults.eval_linup¶ Linear uncertainty propagation
Approximates the variance of output models using a linearization of functions—linear uncertainty propagation. Optionally decomposes the output variance according to additive factors from each input.
Parameters: - model (gr.Model) – Model to evaluate
- df_base (DataFrame or None) – Base levels for evaluation; use “nom” for nominal levels.
- append (bool) – Append results to nominal inputs?
- decomp (bool) – Decompose the fractional variances according to each input?
- decimals (int) – Decimals to report for fractional variances
- n (float) – Monte Carlo sample size, for estimating covariance matrix
- seed (int or None) – Monte Carlo seed
Returns: Output variances at each deterministic level
Return type: DataFrame
Examples:
import grama as gr from grama.models import make_test md = make_test() ## Set manual levels for deterministic inputs; nominal levels for random inputs md >> gr.ev_linup(df_det=gr.df_make(x2=[0, 1, 2]) ## Use nominal deterministic levels md >> gr.ev_linup(df_base="nom")
-
grama.eval_defaults.eval_nominal¶ Evaluate model at nominal values
Evaluates a given model at a model nominal conditions (median) of random inputs. Optionally set nominal values for the deterministic inputs.
Parameters: - model (gr.Model) – Model to evaluate
- df_det (DataFrame or None) – Deterministic levels for evaluation; use “nom” for nominal deterministic levels. If provided model has no deterministic variables (model.n_var_det == 0), then df_det may equal None.
- append (bool) – Append results to nominal inputs?
- skip (bool) – Skip evaluation of the functions?
Returns: Results of nominal model evaluation or unevaluated design
Return type: DataFrame
Examples:
import grama as gr from grama.models import make_test md = make_test() ## Set manual levels for deterministic inputs; nominal levels for random inputs md >> gr.ev_nominal(df_det=gr.df_make(x2=[0, 1, 2]) ## Use nominal deterministic levels md >> gr.ev_nominal(df_det="nom")
-
grama.eval_defaults.eval_grad_fd¶ Finite-difference gradient approximation
Evaluates a given model with a central-difference stencil to approximate the gradient.
Parameters: - model (gr.Model) – Model to differentiate
- h (numeric) – finite difference stepsize, single (scalar): or per-input (array)
- df_base (DataFrame) – Base-points for gradient calculations
- var (list(str) or string) – list of variables to differentiate, or flag; “rand” for var_rand, “det” for var_det
- append (bool) – Append results to base point inputs?
- skip (bool) – Skip evaluation of the functions?
Returns: Gradient approximation or unevaluated design
Return type: DataFrame
- @pre (not isinstance(h, collections.Sequence)) |
- (h.shape[0] == df_base.shape[1])
Examples:
import grama as gr from grama.models import make_cantilever_beam md = make_cantilever_beam() # Select base point(s) df_nom = md >> gr.ev_nominal(df_det="nom") # Approximate the gradient df_grad = md >> gr.ev_grad_fd(df_base=df_nom)
-
grama.eval_defaults.eval_sample¶ Draw a random sample
Evaluates a model with a random sample of the random model inputs. Generates outer product with deterministic levels (common random numbers) OR generates a sample fully-independent of deterministic levels (non-common random numbers).
For more expensive models, it can be helpful to tune n to achieve a reasonable runtime. An even more effective approach is to use skip evaluation along with tran_sp() to evaluate a small, representative sample. (See examples below.)
Parameters: - model (gr.Model) – Model to evaluate
- n (numeric) – number of observations to draw
- df_det (DataFrame or None) – Deterministic levels for evaluation; use “nom” for nominal deterministic levels. If provided model has no deterministic variables (model.n_var_det == 0), then df_det may equal None.
- seed (int) – random seed to use
- append (bool) – Append results to input values?
- skip (bool) – Skip evaluation of the functions?
- comm (bool) – Use common random numbers (CRN) across deterministic levels? CRN will tend to aid in the comparison of statistics across deterministic levels and enhance the convergence of stochastic optimization.
- ind_comm (str or None) – Name of realization index column; not added if None
Returns: Results of evaluation or unevaluated design
Return type: DataFrame
Examples:
import grama as gr from grama.models import make_test DF = gr.Intention() # Simple random sample evaluation md = make_test() df = md >> gr.ev_sample(n=1e2, df_det="nom") df.describe() ## Use autoplot to visualize results ( md >> gr.ev_sample(n=1e2, df_det="nom") >> gr.pt_auto() ) ## Cantilever beam examples from grama.models import make_cantilever_beam md_beam = make_cantilever_beam() ## Use the realization index to facilitate plotting # Try running this without the `group` aesthetic in `geom_line()`; # without the group the plot will not have multiple lines. ( md_beam >> gr.ev_sample( n=20, df_det=gr.df_make(w=3, t=gr.linspace(2, 4, 100)), ind_comm="idx", ) >> gr.ggplot(gr.aes("t", "g_stress")) + gr.geom_line(gr.aes(color="w", group="idx")) ) ## Use iocorr to generate input/output correlation tile plot ( md_beam >> gr.ev_sample(n=1e3, df_det="nom", skip=True) # Generate input/output correlation summary >> gr.tf_iocorr() # Visualize >> gr.pt_auto() ) ## Use support points to reduce model runtime ( md_beam # Generate large input sample but don't evaluate outputs >> gr.ev_sample(n=1e5, df_det="nom", skip=True) # Reduce to a smaller---but representative---sample >> gr.tf_sp(n=50) # Evaluate the outputs >> gr.tf_md(md_beam) ) ## Estimate probabilities ( md_beam # Generate large >> gr.ev_sample(n=1e5, df_det="nom") # Estimate probabilities of failure >> gr.tf_summarize( pof_stress=gr.mean(DF.g_stress <= 0), pof_disp=gr.mean(DF.g_disp <= 0), ) )
-
grama.eval_defaults.eval_conservative¶ Evaluates a given model at conservative input quantiles
Uses model specifications to determine the “conservative” direction for each input, and evaluates the model at the desired quantile. Provided primarily for comparing UQ against pseudo-deterministic design criteria (del Rosario et al.; 2021).
Note that if there is no conservative direction for the given input, the given quantile will be ignored and the median will automatically be selected.
Parameters: - model (gr.Model) – Model to evaluate
- quantiles (numeric) – lower quantile value(s) for conservative evaluation; can be single value for all inputs, array of values for each random variable, or None for default 0.01. values in [0, 0.5]
- df_det (DataFrame or None) – Deterministic levels for evaluation; use “nom” for nominal deterministic levels. If provided model has no deterministic variables (model.n_var_det == 0), then df_det may equal None.
- append (bool) – Append results to conservative inputs?
- skip (bool) – Skip evaluation of the functions?
Returns: Conservative evaluation or unevaluated design
Return type: DataFrame
References
del Rosario, Zachary, Richard W. Fenrich, and Gianluca Iaccarino. “When Are Allowables Conservative?.” AIAA Journal 59.5 (2021): 1760-1772.
Examples:
import grama as gr from grama.models import make_plate_buckle md = make_plate_buckle() # Evaluate at conservative input values md >> gr.ev_conservative(df_det="nom")
grama.eval_opt module¶
-
grama.eval_opt.eval_nls¶ Estimate with Nonlinear Least Squares (NLS)
Estimate best-fit variable levels with nonlinear least squares (NLS).
Parameters: - model (gr.Model) – Model to analyze. All model variables selected for fitting must be bounded or random. Deterministic variables may have semi-infinite bounds.
- df_data (DataFrame) – Data for estimating parameters. Variables not found in df_data optimized in fitting.
- out (list or None) – Output contributions to consider in computing MSE. Assumed to be model.out if left as None.
- var_fix (list or None) – Variables to fix to nominal levels. Note that variables with domain width zero will automatically be fixed.
- df_init (DataFrame or None) – Initial guesses for parameters; overrides
- n_restart (int) –
- append (bool) – Append metadata? (Initial guess, MSE, optimizer status)
- tol (float) – Optimizer convergence tolerance
- n_maxiter (int) – Optimizer maximum iterations
- n_restart – Number of restarts; beyond n_restart=1 random restarts are used.
- seed (int OR None) – Random seed for restarts
- verbose (bool) – Print messages to console?
Returns: Results of estimation
Return type: DataFrame
Examples:
import grama as gr from grama.data import df_trajectory_full from grama.models import make_trajectory_linear md_trajectory = make_trajectory_linear() df_fit = ( md_trajectory >> gr.ev_nls(df_data=df_trajectory_full) ) print(df_fit)
-
grama.eval_opt.eval_min¶ Constrained minimization using functions from a model
Perform constrained minimization using functions from a model. Model must have deterministic variables only.
Wrapper for scipy.optimize.minimize
Parameters: - model (gr.Model) – Model to analyze. All model variables must be deterministic.
- out_min (str) – Output to use as minimization objective.
- out_geq (None OR list of str) – Outputs to use as geq constraints; out >= 0
- out_leq (None OR list of str) – Outputs to use as leq constraints; out <= 0
- out_eq (None OR list of str) – Outputs to use as equality constraints; out == 0
- method (str) – Optimization method; see the documentation for scipy.optimize.minimize for options.
- tol (float) – Optimization objective convergence tolerance
- n_restart (int) – Number of restarts; beyond n_restart=1 random restarts are used.
- df_start (None or DataFrame) – Specific starting values to use; overrides n_restart if non None provided.
Returns: Results of optimization
Return type: DataFrame
Examples:
import grama as gr ## Define a model with objective and constraints md = ( gr.Model("Constrained Rosenbrock") >> gr.cp_function( fun=lambda x: (1 - x[0])**2 + 100*(x[1] - x[0]**2)**2, var=["x", "y"], out=["c"], ) >> gr.cp_function( fun=lambda x: (x[0] - 1)**3 - x[1] + 1, var=["x", "y"], out=["g1"], ) >> gr.cp_function( fun=lambda x: x[0] + x[1] - 2, var=["x", "y"], out=["g2"], ) >> gr.cp_bounds( x=(-1.5, +1.5), y=(-0.5, +2.5), ) ) ## Run the optimizer md >> gr.ev_min( out_min="c", out_leq=["g1", "g2"] )
grama.eval_pnd module¶
-
grama.eval_pnd.approx_pnd(X_pred, X_cov, X_train, signs, n=10000, seed=None)¶ Approximate the PND via mixture importance sampling
Approximate the probability non-dominated (PND) for a set of predictive points using a mixture importance sampling approach. Predictive points are assumed to have predictive gaussian distributions (with specified mean and covariance matrix).
Parameters: - X_pred (2d numpy array) – Predictive values
- X_cov (iterable of 2d numpy arrays) – Predictive covariance matrices
- X_train (2d numpy array) – Training values, used to determine existing Pareto frontier
- signs (numpy array of +/-1 values) – Array of optimization signs: {-1: Minimize, +1 Maximize}
- Kwargs:
- n (int): Number of draws for importance sampler seed (int): Seed for random state
Returns: Estimated PND values var_values (array): Estimated variance values Return type: pr_scores (array) References
Owen Monte Carlo theory, methods and examples (2013)
-
grama.eval_pnd.choice(a, size=None, replace=True, p=None)¶ Generates a random sample from a given 1-D array
New in version 1.7.0.
Note
New code should use the
choicemethod of adefault_rng()instance instead; please see the random-quick-start.Parameters: - a (1-D array-like or int) – If an ndarray, a random sample is generated from its elements.
If an int, the random sample is generated as if it were
np.arange(a) - size (int or tuple of ints, optional) – Output shape. If the given shape is, e.g.,
(m, n, k), thenm * n * ksamples are drawn. Default is None, in which case a single value is returned. - replace (boolean, optional) – Whether the sample is with or without replacement. Default is True,
meaning that a value of
acan be selected multiple times. - p (1-D array-like, optional) – The probabilities associated with each entry in a.
If not given, the sample assumes a uniform distribution over all
entries in
a.
Returns: samples – The generated random samples
Return type: single item or ndarray
Raises: ValueError– If a is an int and less than zero, if a or p are not 1-dimensional, if a is an array-like of size 0, if p is not a vector of probabilities, if a and p have different lengths, or if replace=False and the sample size is greater than the population sizeSee also
randint(),shuffle(),permutation()Generator.choice()- which should be used in new code
Notes
Setting user-specified probabilities through
puses a more general but less efficient sampler than the default. The general sampler produces a different sample than the optimized sampler even if each element ofpis 1 / len(a).Sampling random rows from a 2-D array is not possible with this function, but is possible with Generator.choice through its
axiskeyword.Examples
Generate a uniform random sample from np.arange(5) of size 3:
>>> np.random.choice(5, 3) array([0, 3, 4]) # random >>> #This is equivalent to np.random.randint(0,5,3)
Generate a non-uniform random sample from np.arange(5) of size 3:
>>> np.random.choice(5, 3, p=[0.1, 0, 0.3, 0.6, 0]) array([3, 3, 0]) # random
Generate a uniform random sample from np.arange(5) of size 3 without replacement:
>>> np.random.choice(5, 3, replace=False) array([3,1,0]) # random >>> #This is equivalent to np.random.permutation(np.arange(5))[:3]
Generate a non-uniform random sample from np.arange(5) of size 3 without replacement:
>>> np.random.choice(5, 3, replace=False, p=[0.1, 0, 0.3, 0.6, 0]) array([2, 3, 0]) # random
Any of the above can be repeated with an arbitrary array-like instead of just integers. For instance:
>>> aa_milne_arr = ['pooh', 'rabbit', 'piglet', 'Christopher'] >>> np.random.choice(aa_milne_arr, 5, p=[0.5, 0.1, 0.1, 0.3]) array(['pooh', 'pooh', 'pooh', 'Christopher', 'piglet'], # random dtype='<U11')
- a (1-D array-like or int) – If an ndarray, a random sample is generated from its elements.
If an int, the random sample is generated as if it were
-
grama.eval_pnd.dprop(X, Sigma, X_means)¶ Evaluate the PDF of a mixture proposal distribution
Evaluate the PDF of a gaussian mixture distribution with a common covariance matrix and different means.
Parameters: - X (2d numpy array) – Observations for which to evaluate the density
- Sigma (2d numpy array) – Common covariance matrix for mixture distribution
- X_means (2d numpy array) – Means for mixture distribution
- Preconditions:
- X.shape[1] == X_means.shape[1] Sigma.shape[0] == X_means.shape[1] Sigma.shape[1] == X_means.shape[1]
Returns: Density values Return type: numpy array
-
grama.eval_pnd.eval_pnd¶ Approximate the probability non-dominated (PND)
Approximates the probability non-dominated (PND) for a set of training points given a fitted probabilistic model. Used to rank a set of candidates in the context of multiobjective optimization.
Parameters: - model (gr.model) – predictive model to evaluate
- df_train (DataFrame) – dataframe with training data
- df_test (DataFrame) – dataframe with test data
- signs (dict) – dict with the variables you would like to use and minimization or maximization parameter for each
- append (bool) – Append df_test to pnd algorithm outputs
- Kwargs:
- n (int): Number of draws for importance sampler seed (int): declarble seed value for reproducibility
Returns: Results of predictive model going through a PND algorithm. Conatians both values and their scores. Return type: DataFrame References
del Rosario, Zachary, et al. “Assessing the frontier: Active learning, model accuracy, and multi-objective candidate discovery and optimization.” The Journal of Chemical Physics 153.2 (2020): 024112.
Examples:
import grama as gr ## Define a ground-truth model md_true = gr.make_pareto_random() df_data = ( md_true >> gr.ev_sample(n=2e3, seed=101, df_det="nom") ) ## Generate test/train data df_train = ( df_data >> gr.tf_sample(n=10) ) df_test = ( df_data >> gr.anti_join( df_train, by = ["x1","x2"] ) >> gr.tf_sample(n=200) ) ## Fit a model to training data md_fit = ( df_train >> gr.ft_gp( var=["x1","x2"] out=["y1","y2"] ) ) ## Rank training points by PND algorithm df_pnd = ( md_fit >> gr.ev_pnd( df_train, df_test, signs = {"y1":1, "y2":1}, seed = 101 ) >> gr.tf_arrange(gr.desc(DF.pr_scores)) )
-
grama.eval_pnd.floor_sig(sig, sig_min=1e-08)¶ Floor an array of variances
-
grama.eval_pnd.make_proposal_sigma(X, idx_pareto, X_cov)¶ Estimate parameters for PND importance distribution
Parameters: - X (2d numpy array) – Full set of response values
- idx_pareto (boolean array) – Whether each response value is a Pareto point
- X_cov (iterable of 2d numpy array) – Predictive covariance matrices
- Preconditions:
- X.shape[0] == len(idx_pareto) X_cov[i].shape[0] == X.shape[1] for all valid i X_cov[i].shape[1] == X.shape[1] for all valid i
Returns: Common covariance matrix for PND importance distribution Return type: 2d numpy array
-
grama.eval_pnd.multivariate_normal(mean, cov, size=None, check_valid='warn', tol=1e-8)¶ Draw random samples from a multivariate normal distribution.
The multivariate normal, multinormal or Gaussian distribution is a generalization of the one-dimensional normal distribution to higher dimensions. Such a distribution is specified by its mean and covariance matrix. These parameters are analogous to the mean (average or “center”) and variance (standard deviation, or “width,” squared) of the one-dimensional normal distribution.
Note
New code should use the
multivariate_normalmethod of adefault_rng()instance instead; please see the random-quick-start.Parameters: - mean (1-D array_like, of length N) – Mean of the N-dimensional distribution.
- cov (2-D array_like, of shape (N, N)) – Covariance matrix of the distribution. It must be symmetric and positive-semidefinite for proper sampling.
- size (int or tuple of ints, optional) – Given a shape of, for example,
(m,n,k),m*n*ksamples are generated, and packed in an m-by-n-by-k arrangement. Because each sample is N-dimensional, the output shape is(m,n,k,N). If no shape is specified, a single (N-D) sample is returned. - check_valid ({ 'warn', 'raise', 'ignore' }, optional) – Behavior when the covariance matrix is not positive semidefinite.
- tol (float, optional) – Tolerance when checking the singular values in covariance matrix. cov is cast to double before the check.
Returns: out – The drawn samples, of shape size, if that was provided. If not, the shape is
(N,).In other words, each entry
out[i,j,...,:]is an N-dimensional value drawn from the distribution.Return type: ndarray
See also
Generator.multivariate_normal()- which should be used for new code.
Notes
The mean is a coordinate in N-dimensional space, which represents the location where samples are most likely to be generated. This is analogous to the peak of the bell curve for the one-dimensional or univariate normal distribution.
Covariance indicates the level to which two variables vary together. From the multivariate normal distribution, we draw N-dimensional samples,
![X = [x_1, x_2, ... x_N]](../_images/math/9391bf1d850e8ba701b49624b0ade07272831afd.png) . The covariance matrix
element
. The covariance matrix
element 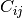 is the covariance of
is the covariance of 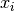 and
and 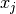 .
The element
.
The element 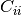 is the variance of
is the variance of 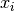 (i.e. its
“spread”).
(i.e. its
“spread”).Instead of specifying the full covariance matrix, popular approximations include:
- Spherical covariance (cov is a multiple of the identity matrix)
- Diagonal covariance (cov has non-negative elements, and only on the diagonal)
This geometrical property can be seen in two dimensions by plotting generated data-points:
>>> mean = [0, 0] >>> cov = [[1, 0], [0, 100]] # diagonal covariance
Diagonal covariance means that points are oriented along x or y-axis:
>>> import matplotlib.pyplot as plt >>> x, y = np.random.multivariate_normal(mean, cov, 5000).T >>> plt.plot(x, y, 'x') >>> plt.axis('equal') >>> plt.show()
Note that the covariance matrix must be positive semidefinite (a.k.a. nonnegative-definite). Otherwise, the behavior of this method is undefined and backwards compatibility is not guaranteed.
References
[1] Papoulis, A., “Probability, Random Variables, and Stochastic Processes,” 3rd ed., New York: McGraw-Hill, 1991. [2] Duda, R. O., Hart, P. E., and Stork, D. G., “Pattern Classification,” 2nd ed., New York: Wiley, 2001. Examples
>>> mean = (1, 2) >>> cov = [[1, 0], [0, 1]] >>> x = np.random.multivariate_normal(mean, cov, (3, 3)) >>> x.shape (3, 3, 2)
The following is probably true, given that 0.6 is roughly twice the standard deviation:
>>> list((x[0,0,:] - mean) < 0.6) [True, True] # random
-
grama.eval_pnd.pareto_min_rel(X_test, X_base=None)¶ Determine if rows in X_test are optimal, compared to X_base
Finds the Pareto-efficient test-points that minimize the column values, relative to a given set of base-points.
Parameters: - X_test (2d numpy array) – Test point observations; rows are observations, columns are features
- X_base (2d numpy array) – Base point observations; rows are observations, columns are features
Returns: Indicates if test observation is Pareto-efficient, relative to base points
Return type: array of boolean values
References
Owen Monte Carlo theory, methods and examples (2013)
-
grama.eval_pnd.rprop(n, Sigma, X_means, seed=None)¶ Draw a sample from gaussian mixture distribution
Draw a sample from a gaussian mixture distribution with a common covariance matrix and different means.
Parameters: - n (int) – Number of observations in sample
- Sigma (2d numpy array) – Common covariance matrix for mixture distribution
- X_means (2d numpy array) – Means for mixture distribution
- Preconditions:
- Sigma.shape[0] == X_means.shape[1] Sigma.shape[1] == X_means.shape[1]
Returns: Sample of observations Return type: 2d numpy array
-
grama.eval_pnd.set_seed()¶ seed(self, seed=None)
Reseed a legacy MT19937 BitGenerator
Notes
This is a convenience, legacy function.
The best practice is to not reseed a BitGenerator, rather to recreate a new one. This method is here for legacy reasons. This example demonstrates best practice.
>>> from numpy.random import MT19937 >>> from numpy.random import RandomState, SeedSequence >>> rs = RandomState(MT19937(SeedSequence(123456789))) # Later, you want to restart the stream >>> rs = RandomState(MT19937(SeedSequence(987654321)))
grama.eval_random module¶
-
grama.eval_random.eval_sinews¶ Sweep study
Perform coordinate sweeps over each model random variable (“sinew” design). Use random starting points drawn from the joint density. Optionally sweep the deterministic variables.
For more expensive models, it can be helpful to tune n_density and n_sweeps to achieve a reasonable runtime.
Use gr.plot_auto() to construct a quick visualization of the output dataframe. Use skip version to visualize the design, and non-skipped version to visualize the results.
Parameters: - model (gr.Model) – Model to evaluate
- n_density (numeric) – Number of points along each sweep
- n_sweeps (numeric) – Number of sweeps per-random variable
- seed (int) – Random seed to use
- df_det (DataFrame) – Deterministic levels for evaluation; use “nom” for nominal deterministic levels, use “swp” to sweep deterministic variables
- varname (str) – Column name to give for sweep variable; default=”sweep_var”
- indname (str) – Column name to give for sweep index; default=”sweep_ind”
- append (bool) – Append results to conservative inputs?
- skip (bool) – Skip evaluation of the functions?
Returns: Results of evaluation or unevaluated design
Return type: DataFrame
Examples:
import grama as gr md = gr.make_cantilever_beam() # Skip evaluation, used to visualize the design (input points) df_design = md >> gr.ev_sinews(df_det="nom", skip=True) df_design >> gr.pt_auto() # Visualize the input-to-output relationships of the model df_sinew = md >> gr.ev_sinews(df_det="nom") df_sinew >> gr.pt_auto()
-
grama.eval_random.eval_hybrid¶ Hybrid points for Sobol’ indices
Use the “hybrid point” design (Sobol’, 1999) to support estimating Sobol’ indices. Use gr.tran_sobol() to post-process the results and compute estimates.
Parameters: - model (gr.Model) – Model to evaluate; must have CopulaIndependence
- n (numeric) – Number of points along each sweep
- plan (str) – Sobol’ index to compute; plan={“first”, “total”}
- seed (int) – Random seed to use
- df_det (DataFrame) – Deterministic levels for evaluation; use “nom” for nominal deterministic levels.
- varname (str) – Column name to give for sweep variable; default=”hybrid_var”
- append (bool) – Append results to conservative inputs?
- skip (bool) – Skip evaluation of the functions?
Returns: Results of evaluation or unevaluated design
Return type: DataFrame
References
I.M. Sobol’, “Sensitivity Estimates for Nonlinear Mathematical Models” (1999) MMCE, Vol 1.
Examples:
import grama as gr md = gr.make_cantilever_beam() ## Compute the first-order indices df_first = md >> gr.ev_hybrid(df_det="nom", plan="first") df_first >> gr.tf_sobol() ## Compute the total-order indices df_total = md >> gr.ev_hybrid(df_det="nom", plan="total") df_total >> gr.tf_sobol()
grama.eval_tail module¶
-
grama.eval_tail.eval_form_pma¶ Tail quantile via FORM PMA
Approximate the desired tail quantiles using the performance measure approach (PMA) of the first-order reliability method (FORM) [1]. Select limit states to minimize at desired quantile with one of: betas (reliability indices), rels (reliability values), or pofs (probabilities of failure). Provide confidence levels cons and estimator covariance df_corr to compute with margin in beta [2].
Note that under the performance measure approach, the optimized limit state value g is sought to be non-negative $g geq 0$. This is usually included as a constraint in optimization, which can be accomplished in by using ``gr.eval_form_pnd()` within a model definition—see the Examples below for more details.
Parameters: - model (gr.Model) – Model to analyze
- df_det (DataFrame) – Deterministic levels for evaluation; use “nom” for nominal deterministic levels.
- betas (dict) – Target reliability indices; key = limit state name; must be in model.out value = reliability index; beta = Phi^{-1}(reliability)
- rels (dict) – Target reliability values; key = limit state name; must be in model.out value = reliability
- pofs (dict) – Target probabilities of failure (POFs); key = limit state name; must be in model.out value = probability of failure; pof = 1 - reliability
- cons (dict or None) – Target confidence levels; key = limit state name; must be in model.out value = confidence level, in (0, 1)
- df_corr (DataFrame or None) – Sampling distribution covariance entries; parameters with no information assumed to be known exactly.
- n_maxiter (int) – Maximum iterations for each optimization run
- n_restart (int) – Number of restarts (== number of optimization runs)
- append (bool) – Append MPP results for random values?
- verbose (bool) – Print optimization results?
Returns: Results of MPP search
Return type: DataFrame
Notes
Since FORM PMA relies on optimization over the limit state, it is often beneficial to scale your limit state to keep values near unity.
References
Tu, Choi, and Park, “A new study on reliability-based design optimization,” Journal of Mechanical Design, 1999 del Rosario, Fenrich, and Iaccarino, “Fast precision margin with the first-order reliability method,” AIAA Journal, 2019
Examples:
import grama as gr from grama.models import make_cantilever_beam md_beam = make_cantilever_beam() ## Evaluate the reliability of specified designs ( md_beam >> gr.ev_form_pma( # Specify target reliability betas=dict(g_stress=3, g_disp=3), # Analyze three different thicknesses df_det=gr.df_make(t=[2, 3, 4], w=3) ) ) ## Specify reliability in POF form ( md_beam >> gr.ev_form_pma( # Specify target reliability pofs=dict(g_stress=1e-3, g_disp=1e-3), # Analyze three different thicknesses df_det=gr.df_make(t=[2, 3, 4], w=3) ) ) ## Build a nested model for optimization under uncertainty md_opt = ( gr.Model("Beam Optimization") >> gr.cp_vec_function( fun=lambda df: gr.df_make(c_area=df.w * df.t), var=["w", "t"], out=["c_area"], name="Area objective", ) >> gr.cp_vec_function( fun=lambda df: gr.eval_form_pma( md_beam, betas=dict(g_stress=3, g_disp=3), df_det=df, append=False, ) var=["w", "t"], out=["g_stress", "g_disp"], name="Reliability constraints", ) >> gr.cp_bounds(w=(2, 4), t=(2, 4)) ) # Run the optimization ( md_opt >> gr.ev_min( out_min="c_area", out_geq=["g_stress", "g_disp"], ) )
-
grama.eval_tail.eval_form_ria¶ Tail reliability via FORM RIA
Approximate the desired tail probability using the reliability index approach (RIA) of the first-order reliability method (FORM) [1]. Select limit states to analyze with list input limits. Choose output type using format argument (betas for reliability indices, rels for realibility values, pofs for probabilify of failure values). Provide confidence levels cons and estimator covariance df_corr to compute with margin in beta [2].
Note that the reliability index approach (RIA) is generally less stable than the performance measure approach (PMA). Consider using
gr.eval_form_pma()instead, particularly when using FORM to optimize a design.Parameters: - model (gr.Model) – Model to analyze
- limits (list) – Target limit states; must be in model.out; limit state assumed to be critical at g == 0.
- format (str) – One of (“betas”, “rels”, “pofs”). Format for computed reliability information
- cons (dict or None) – Target confidence levels; key = limit state name; must be in model.out value = confidence level, in (0, 1)
- df_corr (DataFrame or None) – Sampling distribution covariance entries; parameters with no information assumed to be known exactly.
- df_det (DataFrame) – Deterministic levels for evaluation; use “nom” for nominal deterministic levels.
- n_maxiter (int) – Maximum iterations for each optimization run
- n_restart (int) – Number of restarts (== number of optimization runs)
- append (bool) – Append MPP results for random values?
- verbose (bool) – Print optimization results?
Returns: Results of MPP search
Return type: DataFrame
Notes
Since FORM RIA relies on optimization over the limit state, it is often beneficial to scale your limit state to keep values near unity.
References
[1] Tu, Choi, and Park, “A new study on reliability-based design optimization,” Journal of Mechanical Design, 1999 [2] del Rosario, Fenrich, and Iaccarino, “Fast precision margin with the first-order reliability method,” AIAA Journal, 2019
Examples:
import grama as gr from grama.models import make_cantilever_beam md_beam = make_cantilever_beam() ## Evaluate the reliability of specified designs ( md_beam >> gr.ev_form_ria( # Specify limit states to analyze limits=("g_stress", "g_disp"), # Analyze three different thicknesses df_det=gr.df_make(t=[2, 3, 4], w=3) ) )
grama.fit_synonyms module¶
-
grama.fit_synonyms.fit_nls¶ Fit a model with Nonlinear Least Squares (NLS)
Estimate best-fit variable levels with nonlinear least squares (NLS), and return an executable model with those frozen best-fit levels. Optionally, fit a distribution on the parameters to quantify parametric uncertainty.
Note that it is highly likely you will need to adjust either the bounds of your model or the initial guess of the optimizer (via df_init). Use these to guide the optimizer towards reasonable input values, otherwise you are likely to get nonsensical results.
Note: This is a synonym for eval_nls(); see the documentation for eval_nls() for keyword argument options available beyond those listed here.
Parameters: - df_data (DataFrame) – Data for estimating best-fit variable levels. Variables not found in df_data optimized for fitting.
- md (gr.Model) – Model to analyze. All model variables selected for fitting must be bounded or random. Deterministic variables may have semi-infinite bounds.
- var_fix (list or None) – Variables to fix to nominal levels. Note that variables with domain width zero will automatically be fixed.
- df_init (DataFrame) – Initial guesses for parameters; overrides n_restart
- n_restart (int) – Number of restarts to try; the first try is at the nominal conditions of the model. Returned model will use the least-error parameter set among restarts tested.
- n_maxiter (int) – Optimizer maximum iterations
- verbose (bool) – Print best-fit parameters to console?
- uq_method (str OR None) – If string, select method to quantify parameter uncertainties. If None, provide best-fit values only. Methods: uq_method = “linpool”: assume normal errors; linearly approximate parameter effects; equally pool variance matrices for each output
Returns: - Model for evaluation with best-fit variables frozen to
optimized levels.
Return type: gr.Model
Examples:
import grama as gr from grama.data import df_trajectory_windowed from grama.models import make_trajectory_linear DF = gr.Intention() md_trajectory = make_trajectory_linear() ## Fit md_fitted = ( df_trajectory_windowed >> gr.ft_nls(md=md_trajectory) ) ## Fit, stabilize with initial guess md_fitted = ( df_trajectory_windowed >> gr.ft_nls( md=md_trajectory, df_init=gr.df_make(u0=18, v0=18, tau=16), ) ) ## Fit, and return input uncertainties md_fitted_uq = ( df_trajectory_windowed >> gr.ft_nls( md=md_trajectory, df_init=gr.df_make(u0=18, v0=18, tau=16), uq_method="linpool", ) )
grama.marginals module¶
-
grama.marginals.marg_gkde(data, sign=None)¶ Fit a gaussian KDE to data
Fits a gaussian kernel density estimate (KDE) to data.
Parameters: - data (iterable) – Data for fit
- sign (bool) – Include sign? (Optional)
Returns: Marginal distribution
Return type: gr.MarginalGKDE
Examples:
import grama as gr from grama.data import df_stang md = ( gr.Model("Marginal Example") >> gr.cp_marginals( E=gr.marg_gkde(df_stang.E), mu=gr.marg_gkde(df_stang.mu), ) ) md
-
grama.marginals.marg_fit(dist, data, name=True, sign=None, **kwargs)¶ Fit scipy.stats continuous distirbution
Fits a scipy.stats continuous distribution. Intended to be used to define a marginal distribution from data.
Parameters: - dist (str) – Distribution to fit
- data (iterable) – Data for fit
- name (bool) – Include distribution name?
- sign (bool) – Include sign? (Optional)
- loc (float) – Initial guess for location loc parameter (Optional)
- scale (float) – Initial guess for scale scale parameter (Optional)
- floc (float) – Value to fix the location loc parameter (Optional) Note that for distributions such as “lognorm” or “weibull_min”, setting floc=0 selects the 2-parameter version of the distribution.
- fscale (float) – Value to fix the location scale parameter (Optional)
- f* (float) – Value to fix the specified shape parameter (Optional) e.g. give fc to fix the c parameter
Returns: Distribution
Return type: gr.MarginalNamed
Examples:
import grama as gr from grama.data import df_shewhart # Fit normal distribution mg_normal = gr.marg_named( "norm", df_shewhart.tensile_strength, ) # Fit two-parameter Weibull distribution mg_weibull2 = gr.marg_named( "weibull_min", df_shewhart.tensile_strength, floc=0, # 2-parameter has frozen loc == 0 ) # Fit three-parameter Weibull distribution mg_weibull3 = gr.marg_named( "weibull_min", df_shewhart.tensile_strength, loc=0, # 3-parameter fit tends to be unstable; # an inital guess helps stabilize fit ) # Inspect fits with QQ plot ( df_shewhart >> gr.tf_mutate( q_normal=gr.qqvals(DF.tensile_strength, marg=mg_normal), q_weibull2=gr.qqvals(DF.tensile_strength, marg=mg_weibull2), ) >> gr.tf_pivot_longer( columns=[ "q_normal", "q_weibull2", ], names_to=[".value", "Distribution"], names_sep="_" ) >> gr.ggplot(gr.aes("q", "tensile_strength")) + gr.geom_abline(intercept=0, slope=1, linetype="dashed") + gr.geom_point(gr.aes(color="Distribution")) )
-
grama.marginals.marg_mom(dist, mean=None, sd=None, cov=None, var=None, skew=None, kurt=None, kurt_excess=None, floc=None, sign=0, dict_x0=None)¶ Fit scipy.stats continuous distribution via moments
Fit a continuous distribution using the method of moments. Select a distribution shape and provide numerical values for a convenient set of common moments.
This routine uses a vector-output root finding routine to match the moments. You may set an optional initial guess for the distribution parameters using the dict_x0 argument.
Parameters: dist (str) – Name of distribution to fit - Kwargs:
mean (float): Mean of distribution sd (float): Standard deviation of distribution cov (float): Coefficient of Variation of distribution (sd / mean) var (float): Variance of distribution; only one of sd and var can be provided. skew (float): Skewness of distribution kurt (float): Kurtosis of distribution kurt_excess (float): Excess kurtosis of distribution; kurt_excess = kurt - 3.
Only one of kurt and kurt_excess can be provided.- floc (float or None): Frozen value for location parameter
- Note that for distributions such as “lognorm” or “weibull_min”, setting floc=0 selects the 2-parameter version of the distribution.
sign (-1, 0, +1): Sign dict_x0 (dict): Dictionary of initial parameter guesses
Returns: Distribution Return type: gr.MarginalNamed Examples:
import grama as gr ## Fit a normal distribution mg_norm = gr.marg_mom("norm", mean=0, sd=1) ## Fit a (3-parameter) lognormal distribution mg_lognorm = gr.marg_mom("lognorm", mean=1, sd=1, skew=1) ## Fit a lognormal, controlling kurtosis instead mg_lognorm = gr.marg_mom("lognorm", mean=1, sd=1, kurt=1) ## Fit a 2-parameter lognormal; no skewness or kurtosis needed mg_lognorm = gr.marg_mom("lognorm", mean=1, sd=1, floc=0) ## Not all moment combinations are feasible; this will fail gr.marg_mom("beta", mean=1, sd=1, skew=0, kurt=4) ## Skewness and kurtosis are related for the beta distribution; ## a different combination is feasible gr.marg_mom("beta", mean=1, sd=1, skew=0, kurt=2)
-
class
grama.marginals.Marginal(sign=0)¶ Bases:
abc.ABCParent class for marginal distributions
-
copy()¶
-
d(x)¶
-
fit(data)¶
-
p(x)¶
-
q(p)¶
-
r(n)¶
-
summary()¶
-
grama.mutate_helpers module¶
-
grama.mutate_helpers.abs(*args, **kwargs)¶ Absolute value
-
grama.mutate_helpers.sin(*args, **kwargs)¶ Sine
-
grama.mutate_helpers.cos(*args, **kwargs)¶ Cosine
-
grama.mutate_helpers.tan(*args, **kwargs)¶ Tangent
-
grama.mutate_helpers.log(*args, **kwargs)¶ (Natural) log
-
grama.mutate_helpers.exp(*args, **kwargs)¶ Exponential (e-base)
-
grama.mutate_helpers.sqrt(*args, **kwargs)¶ Square-root
-
grama.mutate_helpers.pow(*args, **kwargs)¶ Power
- Usage:
- q = pow(x, p) := x ^ p
Parameters: - = base (x) –
- = exponent (p) –
-
grama.mutate_helpers.floor(*args, **kwargs)¶ Round downwards to nearest integer
-
grama.mutate_helpers.ceil(*args, **kwargs)¶ Round upwards to nearest integer
-
grama.mutate_helpers.round(*args, **kwargs)¶ Round value to desired precision
Parameters: - x (float or iterable of floats) – Value(s) to round
- decimals (int) – Number of decimal places for rounding; decimals=0 rounds to integers
-
grama.mutate_helpers.as_int(*args, **kwargs)¶ Cast to integer
-
grama.mutate_helpers.as_float(*args, **kwargs)¶ Cast to float
-
grama.mutate_helpers.as_str(*args, **kwargs)¶ Cast to string
-
grama.mutate_helpers.as_factor(*args, **kwargs)¶ Cast to factor
Parameters: - x (pd.Series) – Column to convert
- categories (list) – Categories (levels) of factor (Optional)
- ordered (boolean) – Order the factor?
-
grama.mutate_helpers.as_numeric(*args, **kwargs)¶ Cast to numeric
-
grama.mutate_helpers.fct_reorder(*args, **kwargs)¶ Reorder a factor on another variable
Parameters: - f (iterable OR DataFrame column) – factor to reorder
- x (iterable OR DataFrame column) – variable on which to reorder; specify aggregation method with fun
- fun (function) – aggregation function for reordering, default=median
Returns: Iterable with levels sorted according to x
Return type: Categorical
Examples:
import grama as gr from grama.data import df_diamonds DF = gr.Intention() ( df_diamonds >> gr.tf_mutate(cut=gr.fct_reorder(DF.cut, DF.price)) >> gr.tf_group_by(DF.cut) >> gr.tf_summarize(max=gr.colmax(DF.price), mean=gr.mean(DF.price)) )
-
grama.mutate_helpers.fillna(*args, **kwargs)¶ Wrapper for pandas Series.fillna
(See below for Pandas documentation)
Examples:
import grama as gr X = gr.Intention() df = gr.df_make(x=[1, gr.NaN], y=[2, 3]) df_filled = ( df >> gr.tf_mutate(x=gr.fillna(X.x, 0)) )
Fill NA/NaN values using the specified method.
Parameters: - value (scalar, dict, Series, or DataFrame) – Value to use to fill holes (e.g. 0), alternately a dict/Series/DataFrame of values specifying which value to use for each index (for a Series) or column (for a DataFrame). Values not in the dict/Series/DataFrame will not be filled. This value cannot be a list.
- method ({'backfill', 'bfill', 'pad', 'ffill', None}, default None) – Method to use for filling holes in reindexed Series pad / ffill: propagate last valid observation forward to next valid backfill / bfill: use next valid observation to fill gap.
- axis ({0 or 'index'}) – Axis along which to fill missing values.
- inplace (bool, default False) – If True, fill in-place. Note: this will modify any other views on this object (e.g., a no-copy slice for a column in a DataFrame).
- limit (int, default None) – If method is specified, this is the maximum number of consecutive NaN values to forward/backward fill. In other words, if there is a gap with more than this number of consecutive NaNs, it will only be partially filled. If method is not specified, this is the maximum number of entries along the entire axis where NaNs will be filled. Must be greater than 0 if not None.
- downcast (dict, default is None) – A dict of item->dtype of what to downcast if possible, or the string ‘infer’ which will try to downcast to an appropriate equal type (e.g. float64 to int64 if possible).
Returns: Object with missing values filled or None if
inplace=True.Return type: Series or None
See also
interpolate()- Fill NaN values using interpolation.
reindex()- Conform object to new index.
asfreq()- Convert TimeSeries to specified frequency.
Examples
>>> df = pd.DataFrame([[np.nan, 2, np.nan, 0], ... [3, 4, np.nan, 1], ... [np.nan, np.nan, np.nan, 5], ... [np.nan, 3, np.nan, 4]], ... columns=list("ABCD")) >>> df A B C D 0 NaN 2.0 NaN 0 1 3.0 4.0 NaN 1 2 NaN NaN NaN 5 3 NaN 3.0 NaN 4
Replace all NaN elements with 0s.
>>> df.fillna(0) A B C D 0 0.0 2.0 0.0 0 1 3.0 4.0 0.0 1 2 0.0 0.0 0.0 5 3 0.0 3.0 0.0 4
We can also propagate non-null values forward or backward.
>>> df.fillna(method="ffill") A B C D 0 NaN 2.0 NaN 0 1 3.0 4.0 NaN 1 2 3.0 4.0 NaN 5 3 3.0 3.0 NaN 4
Replace all NaN elements in column ‘A’, ‘B’, ‘C’, and ‘D’, with 0, 1, 2, and 3 respectively.
>>> values = {"A": 0, "B": 1, "C": 2, "D": 3} >>> df.fillna(value=values) A B C D 0 0.0 2.0 2.0 0 1 3.0 4.0 2.0 1 2 0.0 1.0 2.0 5 3 0.0 3.0 2.0 4
Only replace the first NaN element.
>>> df.fillna(value=values, limit=1) A B C D 0 0.0 2.0 2.0 0 1 3.0 4.0 NaN 1 2 NaN 1.0 NaN 5 3 NaN 3.0 NaN 4
When filling using a DataFrame, replacement happens along the same column names and same indices
>>> df2 = pd.DataFrame(np.zeros((4, 4)), columns=list("ABCE")) >>> df.fillna(df2) A B C D 0 0.0 2.0 0.0 0 1 3.0 4.0 0.0 1 2 0.0 0.0 0.0 5 3 0.0 3.0 0.0 4
-
grama.mutate_helpers.qnorm(*args, **kwargs)¶ Normal quantile function (inverse CDF)
-
grama.mutate_helpers.pnorm(*args, **kwargs)¶ Normal cumulative distribution function (CDF)
-
grama.mutate_helpers.dnorm(*args, **kwargs)¶ Normal probability density function (PDF)
-
grama.mutate_helpers.pareto_min(*args, **kwargs)¶ Determine if observation is a Pareto point
Find the Pareto-efficient points that minimize the provided features.
Parameters: xi (iterable OR gr.Intention()) – Feature to minimize; use -X to maximize Returns: Indicates if observation is Pareto-efficient Return type: np.array of boolean
-
grama.mutate_helpers.stratum_min(*args, **kwargs)¶ Compute Pareto stratum number
Compute the Pareto stratum number for a given dataset.
Parameters: - xi (iterable OR gr.Intention()) – Feature to minimize; use -X to maximize
- max_depth (int) – Maximum depth for recursive computation; stratum numbers exceeding this value will not be computed and will be flagged as NaN.
Returns: Pareto stratum number
Return type: np.array of floats
References
del Rosario, Rupp, Kim, Antono, and Ling “Assessing the frontier: Active learning, model accuracy, and multi-objective candidate discovery and optimization” (2020) J. Chem. Phys.
-
grama.mutate_helpers.qqvals(*args, **kwargs)¶ Generate theoretical quantiles
Generate theoretical quantiles for a Q-Q plot. Can provide either a pre-defined Marginal object or the name of a distribution to fit.
Parameters: x (array-like or gr.Intention()) – Target observations
Keyword Arguments: - dist (str or None) – Name of scipy distribution to fit; see gr.valid_dist for list of valid distributions
- marg (gr.Marginal() or None) – Pre-fitted marginal
Returns: Theoretical quantiles, matched in order with target observations
Return type: Series
References
Filliben, J. J., “The Probability Plot Correlation Coefficient Test for Normality” (1975) Technometrics. DOI: 10.1080/00401706.1975.10489279
Examples:
import grama as gr from grama.data import df_shewhart DF = gr.Intention() ## Make a Q-Q plot ( df_shewhart >> gr.tf_mutate(q=gr.qqvals(DF.tensile_strength, dist="norm")) >> gr.ggplot(gr.aes("q", "tensile_strength")) + gr.geom_abline(intercept=0, slope=1, linetype="dashed") + gr.geom_point() ) ## Fit a marginal, use in Q-Q plot mg_tys = gr.marg_fit("lognorm", df_shewhart.tensile_strength, floc=0) # Plot to assess the fit ( df_shewhart >> gr.tf_mutate(q=gr.qqvals(DF.tensile_strength, marg=mg_tys)) >> gr.ggplot(gr.aes("q", "tensile_strength")) + gr.geom_abline(intercept=0, slope=1, linetype="dashed") + gr.geom_point() )
-
grama.mutate_helpers.linspace(*args, **kwargs)¶ Linearly-spaced values
Create an array of linearly-spaced values. Accepts keyword arguments for numpy.linspace.
Parameters: - a (numeric) – Smallest value
- b (numeric) – Largest value
- n (int) – Number of points
Returns: Array of requested values
Return type: numpy array
Notes
This is a symbolic alias for np.linspace(); you can use this in pipe-enabled functions.
Examples:
import grama as gr from grama.data import df_stang DF = gr.Intention() ( df_stang >> gr.tf_mutate(c=gr.linspace(0, 1, gr.n(DF.index))) )
-
grama.mutate_helpers.logspace(*args, **kwargs)¶ Logarithmically-spaced values
Create an array of logarithmically-spaced values. Accepts keyword arguments for numpy.logspace.
Parameters: - a (numeric) – Smallest value
- b (numeric) – Largest value
- n (int) – Number of points
Returns: Array of requested values
Return type: numpy array
Notes
This is a symbolic alias for np.logspace(); you can use this in pipe-enabled functions.
Examples:
import grama as gr from grama.data import df_stang DF = gr.Intention() ( df_stang >> gr.tf_mutate(c=gr.logspace(0, 1, gr.n(DF.index))) )
-
grama.mutate_helpers.consec(*args, **kwargs)¶ Flag consecutive runs of True values
Flag as True all entries associated with a “run” of True values. A “run” is defined as a user-defined count (given by i) of consecutive True values.
Parameters: - series (pd.Series) – Series of boolean values
- i (int) – User-defined count to define a run
Returns: Boolean series flagging consecutive True values
Return type: series
grama.plot_auto module¶
-
grama.plot_auto.plot_contour¶ Plot 2d contours
Plot contours. Usually called as a dispatch from plot_auto().
Parameters: - var (array of str) – Variables for plot axes
- out (str) – Name of output identifier column
- level (str) – Name of level identifier column
- aux (bool) – Auxillary variables present?
- color (str) – Color mode; options: “full”, “bw”
Returns: Contour image
Return type: ggplot
Examples:
import grama as gr from grama.models import make_cantilever_beam md_beam = make_cantilever_beam() ( md_beam >> gr.ev_contour( var=["w", "t"], out=["g_stress"], # Set auxilliary inputs to nominal levels df=gr.eval_nominal(md_beam, df_det="nom"), ) >> gr.pt_auto() )
-
grama.plot_auto.plot_corrtile¶
-
grama.plot_auto.plot_scattermat¶ Create a scatterplot matrix
Create a scatterplot matrix. Often used to visualize a design (set of inputs points) before evaluating the functions.
Usually called as a dispatch from plot_auto().
Parameters: - var (list of strings) – Variables to plot
- color (str) – Color mode; value ignored as default vis is black & white
Returns: Scatterplot matrix
Return type: ggplot
Examples:
import grama as gr from grama.models import make_cantilever_beam md_beam = make_cantilever_beam() ## Dispatch from autoplotter ( md_beam >> gr.ev_sample(n=100, df_det="nom", skip=True) >> gr.pt_auto() ) ## Re-create plot without metadata ( md_beam >> gr.ev_sample(n=100, df_det="nom") >> gr.pt_scattermat(var=md.var) )
-
grama.plot_auto.plot_hists¶ Construct histograms
Create a set of histograms. Often used to visualize the results of random sampling for multiple outputs.
Usually called as a dispatch from plot_auto().
Parameters: - out (list of strings) – Variables to plot
- color (str) – Color mode; value ignored as default vis is black & white
Returns: Seaborn histogram plot
Examples:
import grama as gr from grama.models import make_cantilever_beam md_beam = make_cantilever_beam() ## Dispatch from autoplotter ( md_beam >> gr.ev_sample(n=100, df_det="nom") >> gr.pt_auto() ) ## Re-create without metadata ( md_beam >> gr.ev_sample(n=100, df_det="nom") >> gr.pt_hists(out=md.out) )
-
grama.plot_auto.plot_sinew_inputs¶ Inspect a sinew design
Create a scatterplot matrix with hues. Often used to visualize a sinew design before evaluating the model functions.
Usually called as a dispatch from plot_auto().
Parameters: - df (Pandas DataFrame) – Input design data
- var (list of strings) – Variables to plot
- sweep_ind (string) – Sweep index column in df
- color (str) – Color mode; options: “full”, “bw”
Returns: Seaborn scatterplot matrix
Examples:
import grama as gr from grama.models import make_cantilever_beam md_beam = make_cantilever_beam() ## Dispatch from autoplotter ( md_beam >> gr.ev_sinews(df_det="swp", skip=True) >> gr.pt_auto() ) ## Re-create without metadata ( md_beam >> gr.ev_sinews(df_det="swp") >> gr.pt_sinew_inputs(var=md.var) )
-
grama.plot_auto.plot_sinew_outputs¶ Construct sinew plot
Create a relational lineplot with hues for each sweep. Often used to visualize the outputs of a sinew design.
Usually called as a dispatch from plot_auto().
Parameters: - df (Pandas DataFrame) – Input design data with output results
- var (list of strings) – Variables to plot
- out (list of strings) – Outputs to plot
- sweep_ind (string) – Sweep index column in df
- sweep_var (string) – Swept variable column in df
- color (str) – Color mode; options: “full”, “bw”
Returns: Relational lineplot
Examples:
import grama as gr from grama.models import make_cantilever_beam md_beam = make_cantilever_beam() ## Dispatch from autoplotter ( md_beam >> gr.ev_sinews(df_det="swp") >> gr.pt_auto() ) ## Re-create without metadata ( md_beam >> gr.ev_sinews(df_det="swp") >> gr.pt_sinew_inputs(var=md.var, out=md.out) )
-
grama.plot_auto.plot_auto¶ Automagic plotting
Convenience tool for various grama outputs. Prints delegated plotting function, which can be called manually with different arguments for more tailored plotting.
Parameters: - df (DataFrame) – Data output from appropriate grama routine. See gr.plot_list.keys() for list of supported methods.
- color (str) – Color mode; options: “full”, “bw”
Returns: Plot results
grama.spc module¶
-
grama.spc.c_sd(n)¶ Anti-biasing constant for aggregate standard deviation
Returns the anti-biasing constant for aggregated standard deviation estimates. If the average of $k$ samples each size $n$ are averaged to produce $overline{S} = (1/k) sum_{i=1}^k S_i$, then the de-biased standard deviation is:
$$hat{sigma} = overline{S} / c(n)$$Parameters: n (int) – Sample (batch) size Returns: anti-biasing constant Return type: float References
Kenett and Zacks, Modern Industrial Statistics (2014) 2nd Ed
-
grama.spc.B3(n)¶ Lower Control Limit constant for standard deviation
Returns the Lower Control Limit (LCL) constant for aggregated standard deviation estimates. If the average of $k$ samples each size $n$ are averaged to produce $overline{S} = (1/k) sum_{i=1}^k S_i$, then the LCL is:
$$LCL = B_3 overline{S}$$Parameters: n (int) – Sample (batch) size Returns: LCL constant Return type: float References
Kenett and Zacks, Modern Industrial Statistics (2014) 2nd Ed, Equation (8.22)
-
grama.spc.B4(n)¶ Upper Control Limit constant for standard deviation
Returns the Upper Control Limit (UCL) constant for aggregated standard deviation estimates. If the average of $k$ samples each size $n$ are averaged to produce $overline{S} = (1/k) sum_{i=1}^k S_i$, then the UCL is:
$$UCL = B_4 overline{S}$$Parameters: n (int) – Sample (batch) size Returns: UCL constant Return type: float References
Kenett and Zacks, Modern Industrial Statistics (2014) 2nd Ed, Equation (8.22)
-
grama.spc.plot_xbs(df, group, var, n_side=9, n_delta=6, color='full')¶ Construct Xbar and S chart
Construct an Xbar and S chart to assess the state of statistical control of a dataset.
Parameters: - df (DataFrame) – Data to analyze
- group (str) – Variable for grouping
- var (str) – Variable to study
Keyword Arguments: - n_side (int) – Number of consecutive runs above/below centerline to flag
- n_delta (int) – Number of consecutive runs increasing/decreasing to flag
- color (str) – Color mode; “full” for full color, “bw” for greyscale
Returns: Xbar and S chart
Return type: plotnine object
Examples:
import grama as gr DF = gr.Intention() from grama.data import df_shewhart ( df_shewhart >> gr.tf_mutate(idx=DF.index // 10) >> gr.pt_xbs("idx", "tensile_strength") )
grama.string_helpers module¶
-
grama.string_helpers.str_c(*args, **kwargs)¶ Concatenate strings
-
grama.string_helpers.str_count(*args, **kwargs)¶ Count the number of matches in a string.
-
grama.string_helpers.str_detect(*args, **kwargs)¶ Detect the presence of a pattern match in a string.
-
grama.string_helpers.str_extract(*args, **kwargs)¶ Extract the first regex pattern match
-
grama.string_helpers.str_locate(*args, **kwargs)¶ Find the indices of all pattern matches.
-
grama.string_helpers.str_replace(*args, **kwargs)¶ Replace the first matched pattern in each string.
-
grama.string_helpers.str_replace_all(*args, **kwargs)¶ Replace all occurences of pattern in each string.
-
grama.string_helpers.str_sub(*args, **kwargs)¶ Extract substrings
-
grama.string_helpers.str_split(*args, **kwargs)¶ Split string into list on pattern
Parameters: - string (str or iterable[str]) – String(s) to split
- pattern (str) – Regex pattern on which to split
- Kwargs:
- maxsplit (int): Maximum number of splits, or 0 for unlimited
- Returns
- str or iterable[str]: List (of lists) of strings
-
grama.string_helpers.str_which(*args, **kwargs)¶ Find the index of the first pattern match.
-
grama.string_helpers.str_to_lower(*args, **kwargs)¶ Make string lower-case
Parameters: string (str or iterable[str]) – String(s) to modify - Returns
- str or iterable[str]: List (of lists) of strings
-
grama.string_helpers.str_to_upper(*args, **kwargs)¶ Make string upper-case
Parameters: string (str or iterable[str]) – String(s) to modify - Returns
- str or iterable[str]: List (of lists) of strings
-
grama.string_helpers.str_to_snake(*args, **kwargs)¶ Make string snake case
Parameters: string (str or iterable[str]) – String(s) to modify - Returns
- str or iterable[str]: List (of lists) of strings
grama.support module¶
-
grama.support.tran_sp¶ Compact a dataset with support points
Parameters: - df (DataFrame) – dataset to compact
- n (int) – number of samples for compacted dataset
- var (list of str) – list of variables to compact, must all be numeric
- n_maxiter (int) – maximum number of iterations for support point algorithm
- tol (float) – convergence tolerance
- verbose (bool) – print messages to the console?
- standardize (bool) – standardize columns before running sp? (Restores after sp)
Returns: dataset compacted with support points
Return type: DataFrame
References
Mak and Joseph, “Support Points” (2018) The Annals of Statistics
Examples:
import grama as gr # Compact an existing dataset from grama.data import df_diamonds df_sp = gr.tran_sp(df_diamonds, n=50, var=["price", "carat"]) # Use support points to reduce model runtime from grama.models import make_cantilever_beam md_beam = make_cantilever_beam() ( md_beam ## Generate input sample but don't evaluate outputs >> gr.ev_sample(n=1e4, df_det="nom", skip=True) ## Reduce to a smaller---but representative---sample >> gr.tf_sp(n=50) ## Evaluate the outputs >> gr.tf_md(md_beam) )
grama.tools module¶
-
grama.tools.add_pipe(fun)¶
-
grama.tools.copy_meta(df_source, df_target)¶ Internal metadata copy tool
Parameters: - df_source (DataFrame) – Original dataframe
- df_target (DataFrame) – Target dataframe; receives metadata
Returns: df_target with copied metadata
Return type: DataFrame
-
grama.tools.custom_formatwarning(msg, *args, **kwargs)¶
-
grama.tools.lookup(df, row_labels, col_labels)¶ 2D lookup function for a dataframe (Old Pandas Lookup Method)
Parameters: - df (DataFrame) – DataFrame for lookup
- row_labels (List) – Row labels to use for lookup.
- col_labels (List) – Column labels to use for lookup.
Returns: Found values
Return type: numpy.ndarray
-
grama.tools.hide_traceback()¶ Configure Jupyter to hide error traceback
-
class
grama.tools.pipe(function)¶ Bases:
object
-
grama.tools.tran_outer¶ Outer merge
Perform an outer-merge on two dataframes.
Parameters: - df (DataFrame) – Data to merge
- df_outer (DataFrame) – Data to merge; outer
Returns: Merged data
Return type: DataFrame
Examples:
import grama as gr import pandas as pd df = pd.DataFrame(dict(x=[1,2])) df_outer = pd.DataFrame(dict(y=[3,4])) df_res = gr.tran_outer(df, df_outer) df_res x y 0 1 3 1 2 3 2 1 4 3 2 4
grama.tran_is module¶
-
grama.tran_is.tran_reweight¶ Reweight a sample using likelihood ratio
Reweight is a tool to facilitate “What If?” Monte Carlo simulation; specifically, to make testing a models with the same function(s) but different distributions more computationally efficient.
This tool automates calulation of the likelihood ratio between the distributions of two given models. Using the resulting weights to scale (elementwise multiply) output values and compute summaries is called importance sampling, enabling “What If?” testing. Use of this tool enables one to generate a single Monte Carlo sample, rather than multiple samples for each “What If?” scenario (avoiding extraneous function evaluations).
Let y be a generic output of the scenario. The importance sampling procedure is as follows:
- Create a base scenario represented by md_base, and a desired number of alternative “What If?” scenarios represented my other models.
- Use gr.eval_monte_carlo to generate a single sample df_base of size n using the base scenario md_base. Compute statistics of interest on the output y for this base scenario.
- For each alternative scenario md_new, use gr.tran_reweight to generate weights weight, and use the tool n_e = gr.neff_is(DF.weight) to compute the effective sample size. If n_e << n, then importance sampling is unlikely to give an accurate estimate for this scenario.
- For each alternative scenario md_new, use the relevant weights weight to scale the output value y_new = y * weight, and compute statistics of interest of the weighted output values.
Parameters: Returns: Original df_base with added column of weights.
Return type: DataFrame
Notes
- The base scenario md_base should have fatter tails than any of the scenarios considered as df_new. See Owen (2013) Chapter 9 for more details.
References
A.B. Owen, “Monte Carlo theory, methods and examples” (2013)
Examples:
import grama as gr from grama.models import make_cantilever_beam DF = gr.Intention() md_base = make_cantilever_beam() md_new = ( md_base >> gr.cp_marginals( H=dict(dist="norm", loc=500.0, scale=50.0), ) ) ## Assess safety via simple Monte Carlo df_base = gr.eval_monte_carlo(md_base, df_det="nom", n=1e3) print( df_base >> gr.tf_summarize( pof_stress=gr.mean(DF.g_stress <= 0), pof_disp=gr.mean(DF.g_disp <= 0), ) ) ## Re-use samples to test another scenario print( df_base >> gr.tf_reweight(md_base=md_base, md_new=md_new) >> gr.tf_summarize( pof_stress=gr.mean((DF.g_stress <= 0) * DF.weight), pof_disp=gr.mean((DF.g_disp <= 0) * DF.weight), n_eff=gr.neff_is(DF.weight), ) ) ## It is unsafe to study new scenarios with wider uncertainty than the base scenario md_poor = ( md_base >> gr.cp_marginals( H=dict(dist="norm", loc=500.0, scale=400.0), ) ) ## Note the tiny effective sample size in this case print( md_base >> gr.ev_monte_carlo(n=1e3, df_det="nom") >> gr.tf_reweight(md_base=md_base, md_new=md_poor) >> gr.tf_summarize( pof_stress=gr.mean((DF.g_stress <= 0) * DF.weight), pof_disp=gr.mean((DF.g_disp <= 0) * DF.weight), n_eff=gr.neff_is(DF.weight), ) )
grama.tran_pivot module¶
-
grama.tran_pivot.tran_pivot_longer(df, columns, index_to=None, names_to=None, names_sep=None, names_pattern=None, values_to=None)¶ Lengthen a dataset
“Lengthens” data by increasing the number of rows and decreasing the number of columns.
Parameters: - df (DataFrame) – DataFrame passed through
- columns (str) – Label of column(s) to pivot into longer format
- index_to (str) – str name to create a new representation index of observations; Optional.
- names_to (str) –
name to use for the ‘variable’ column, if None frame.columns.name is used or ‘variable’
- .value indicates that component of the name defines the name of the column containing the cell values, overriding values_to
- names_sep (str OR list of int) –
delimter to seperate the values of the argument(s) from the ‘columns’ parameter into 2 new columns with those values split by that delimeter
- Regex expression is a valid input for names_sep
- names_pattern (str) – Regular expression with capture groups to define targets for names_to.
- values_to (str) – name to use for the ‘value’ column; overridden if “.value” is provided in names_to argument.
Notes
Only one of names_sep OR names_pattern may be given.
Returns: result of being pivoted into a longer format Return type: DataFrame Examples:
import grama as gr ## Simple example ( gr.df_make( A=[1, 2, 3], B=[4, 5, 6], C=[7, 8, 9], ) >> gr.tf_pivot_longer( columns=["A", "B", "C"], names_to="variable", values_to="value", ) ) ## Matching columns on patterns ( gr.df_make( x1=[1, 2, 3], x2=[4, 5, 6], x3=[7, 8, 9], ) >> gr.tf_pivot_longer( columns=gr.matches("\d+"), names_to="variable", values_to="value", ) ) ## Separating column names and data on a names_pattern ( gr.df_make( E00=[1, 2, 3], E45=[4, 5, 6], E90=[7, 8, 9], ) >> gr.tf_pivot_longer( columns=gr.matches("\d+"), names_to=[".value", "angle"], names_pattern="(E)(\d+)", ) )
-
grama.tran_pivot.tran_pivot_wider(df, names_from, indexes_from=None, values_from=None)¶ Widen a dataset
“Widens” data by increasing the number of columns and decreasing the number of rows.
Parameters: - df (DataFrame) – DataFrame passed through
- names_from (str) – Column(s) name(s) to use to make new columns
- indexes_from (str) – Column(s) to use to make new index, if None will preserve and use unspecified columns as index
- values_from (str) – Column(s) to use as new values column(s)
Returns: result of being pivoted wider
Return type: DataFrame
Examples:
import grama as gr ## Simple example ( gr.df_make(var=["x", "x", "y", "y"], value=[0, 1, 2, 3]) >> gr.tf_pivot_wider( names_from="var", values_from="value", ) (
grama.tran_shapley module¶
-
grama.tran_shapley.tran_shapley_cohort¶ Compute cohort shapley values
Assess the impact of each variable on selected observations via cohort shapley [1]. Shapley values are a game-theoretic way to assess the importance of input variables (var) on each of a set of outputs (out). Since values are computed on each observation, cohort shapley can distinguish cases where a variable has a positive impact on one observation, and a negative impact on a different observation.
Note that cohort shapley is combinatorialy expensive in the number of variables, and this expense is multiplied by the number of observations. Use with caution in cases of high dimensionality. Consider using the inds argument to analyze a small subset of your observations.
Parameters: - df (DataFrame) – Variable and output data to analyze
- var (list of strings) – Input variables
- out (list of strings) – Outputs variables
- bins (integer) – Number of “bins” to define coordinate refinement distance
- inds (iterable of indices or None) – Indices of rows to analyze
References
[1] Mase, Owen, and Seiler, “Explaining black box decisions by Shapley cohort refinement” (2019) Arxiv
Examples:
import grama as gr from grama.data import df_stang DF = gr.Intention() # Analyze all observations ( gr.tran_shapley_cohort( df_stang, var=["thick", "ang"], out=["E"], ) >> gr.tf_bind_cols(df_stang) >> gr.tf_filter(DF.E_thick < 0) ) # Compute subset of values ( gr.tran_shapley_cohort( df_stang, var=["thick", "ang"], out=["E"], inds=( df_stang >> gr.tf_filter(DF.thick > 0.08) ).index ) >> gr.tf_bind_cols(df_stang) )
grama.tran_summaries module¶
-
grama.tran_summaries.tran_asub¶ Active subspace estimator
Compute principal directions and eigenvalues for all outputs based on output of ev_grad_fd() to estimate the /active subspace/ (Constantine, 2015).
See also
gr.tran_polyridge()for a gradient-free approach to approximating the active subspace.Parameters: - df (DataFrame) – Gradient evaluations
- prefix (str) – Column name prefix; default=”D”
- outvar (str) – Name to give output id column; default=”output”
- lambvar (str) – Name to give eigenvalue column; default=”lam”
Returns: Active subspace directions and eigenvalues
Return type: DataFrame
References
Constantine, “Active Subspaces” (2015) SIAM
Examples:
import grama as gr from grama.models import make_cantilever_beam md = make_cantilever_beam() df_base = md >> gr.ev_sample(n=1e2, df_det="nom", skip=True) df_grad = md >> gr.ev_grad_fd(df_base=df_base) df_as = df_grad >> gr.tf_asub()
-
grama.tran_summaries.tran_describe¶ Describe a dataframe
Synonym for Pandas df.describe()
Parameters: df (DataFrame) – Data to describe Returns: Printed summary
-
grama.tran_summaries.tran_inner¶ Inner products
Compute inner product of target df with weights defined by df_weights.
Parameters: - df (DataFrame) – Data to compute inner products against
- df_weights (DataFrame) – Weights for inner prodcuts
- prefix (str) – Name prefix for resulting inner product columns; default=”dot”
- name (str) – Name of identity column in df_weights or None
- append (bool) – Append new data to original DataFrame?
Returns: Results of inner products
Return type: DataFrame
Examples:
## Setup import grama as gr DF = gr.Intention() ## PCA example from grama.data import df_diamonds # Compute PCA weights df_weights = gr.tran_pca( df_diamonds >> gr.tf_sample(1000), var=["x", "y", "z", "carat"], ) # Visualize ( df_diamonds >> gr.tf_inner(df_weights=df_weights) >> gr.ggplot(gr.aes("dot0", "dot1")) + gr.geom_point() ) ## Active subspace example from grama.models import make_cantilever_beam md_beam = make_cantilever_beam() # Approximate the active subspace df_data = gr.ev_sample(md_beam, n=1e2, df_det="nom") df_weights = gr.tran_polyridge( df_data, var=md_beam.var_rand, # Use meaningful predictors only out="g_disp", # Target g_disp for reduction n_degree=2, n_degree=1, ) # Construct shadow plot; use tran_inner to calculate active variable ( df_data >> gr.tf_inner(df_weights=df_weights) >> gr.ggplot(gr.aes("dot", "g_disp")) + gr.geom_point() )
-
grama.tran_summaries.tran_pca¶ Principal Component Analysis
Compute principal directions and eigenvalues for a dataset. Can specify columns to analyze, or just analyze all numerical columns.
Parameters: - df (DataFrame) – Data to analyze
- var (list of str or None) – List of columns to analyze
- lambvar (str) – Name to give eigenvalue column; default=”lam”
- standardize (bool) – Standardize columns? default=False
Returns: principal directions and eigenvalues
Return type: DataFrame
References
TODO
Examples:
import grama as gr from grama.data import df_stang df_pca = df_stang >> gr.tf_pca()
-
grama.tran_summaries.tran_sobol¶ Post-process results from gr.eval_hybrid()
Estimate Sobol’ indices based on hybrid point evaluations (Sobol’, 1999). Intended as post-processor for gr.eval_hybrid().
Parameters: - df (DataFrame) – Hybrid point results from gr.eval_hybrid()
- typename (str) – Name to give index type column in results
- digits (int) – Number of digits for rounding reported results
- full (bool) – Return un-normalized indices and variance?
Returns: Sobol’ indices
Return type: DataFrame
Notes
- Index type [“first”, “total”] is inferred from input df._meta; this is assigned by gr.eval_hybrid().
- Index normalization coded in the “ind” column; S: Normalized index T: Un-normalized index var: Total variance
References
I.M. Sobol’, “Sensitivity Estimates for Nonlinear Mathematical Models” (1999) MMCE, Vol 1.
Examples:
import grama as gr from grama.models import make_cantilever_beam md = make_cantilever_beam() df_first = md >> gr.ev_hybrid(df_det="nom", plan="first") df_first >> gr.tf_sobol() df_total = md >> gr.ev_hybrid(df_det="nom", plan="total") df_total >> gr.tf_sobol()
-
grama.tran_summaries.tran_iocorr¶ Compute input-output correlations
Compute all correlations between input and output quantities.
Parameters: - df (DataFrame) – Data to summarize
- var (iterable of strings) – Column names for inputs
- out (iterable of strings) – Column names for outputs
- method (str) – Method for correlation; one of “pearson” or “spearman”
Returns: Correlations between each input and output
Return type: DataFrame
grama.tran_tools module¶
-
grama.tran_tools.tran_angles(df, df2)¶ Subspace angles
Compute the subspace angles between two matrices. A wrapper for scipy.linalg.subspace_angles that corrects for column ordering. Row ordering is assumed.
Parameters: - df (DataFrame) – First matrix to compare
- df2 (DataFrame) – Second matrix to compare
Returns: Array of angles (in radians)
Return type: array
Examples:
import grama as gr import pandas as pd df = pd.DataFrame(dict(v=[+1, +1])) df_v1 = pd.DataFrame(dict(w=[+1, -1])) df_v2 = pd.DataFrame(dict(w=[+1, +1])) theta1 = angles(df, df_v1) theta2 = angles(df, df_v2)
-
grama.tran_tools.tran_bootstrap¶ Estimate bootstrap confidence intervals
Estimate bootstrap confidence intervals for a given transform. Uses the “bootstrap-t” procedure discussed in Efron and Tibshirani (1993).
Parameters: - df (DataFrame) – Data to bootstrap
- tran (grama tran_ function) – Transform procedure which generates statistic
- n_boot (numeric) – Monte Carlo resamples for bootstrap
- n_sub (numeric) – Nested resamples to estimate SE
- con (float) – Confidence level
- col_sel (list(string)) – Columns to include in bootstrap calculation
Returns: Results of tran(df), plus _lo and _up columns for numeric columns
Return type: DataFrame
- References and notes:
- Efron and Tibshirani (1993) “The bootstrap-t procedure… is particularly applicable to location statistics like the sample mean…. The bootstrap-t method, at least in its simple form, cannot be trusted for more general problems, like setting a confidence interval for a correlation coefficient.”
Examples:
-
grama.tran_tools.tran_copula_corr(df, model=None, density=None)¶ Compute Gaussian copula correlations from data
Convenience function to fit a Gaussian copula (correlations) based on data and pre-fitted marginals. Intended for use with
gr.comp_copula_gaussian(). Must provide either model or density.Note: This is called automatically when you provide a dataset to
gr.comp_copula_gaussian().Parameters: - df (DataFrame) – Matrix of data for correlation estimation
- model (gr.Model) – Model with defined marginals
- density (gr.Density) – Density with defined marginals
Returns: Correlation data ready for use with
gr.comp_copula_gaussian()Return type: DataFrame
Examples:
import grama as gr from grama.data import df_stang ## Verbose, manual approach md = ( gr.Model() >> gr.cp_marginals( E=gr.marg_named(df_stang.E, "norm"), mu=gr.marg_named(df_stang.mu, "beta"), thick=gr.marg_named(df_stang.thick, "norm"), ) ) df_corr = gr.tran_copula_corr(df_stang, model=md) md = gr.comp_copula_gaussian(md, df_corr=df_corr) ## Automatic approach md = ( gr.Model() >> gr.cp_marginals( E=gr.marg_named(df_stang.E, "norm"), mu=gr.marg_named(df_stang.mu, "beta"), thick=gr.marg_named(df_stang.thick, "norm"), ) >> gr.cp_copula_gaussian(df_data=df_stang) )
-
grama.tran_tools.tran_kfolds¶ Perform k-fold CV
Perform k-fold cross-validation (CV) using a given fitting procedure (ft). Optionally provide a fold identifier column, or (randomly) assign folds.
Parameters: - df (DataFrame) – Data to pass to given fitting procedure
- ft (gr.ft_) – Partially-evaluated grama fit function; defines model fitting procedure and outputs to aggregate
- tf (gr.tf_) – Partially-evaluated grama transform function; evaluation of fitted model will be passed to tf and provided with keyword arguments from summaries
- out (list or None) – Outputs for which to compute summaries; None uses ft.out
- var_fold (str or None) – Column to treat as fold identifier; overrides k
- suffix (str) – Suffix for predicted value; used to distinguish between predicted and actual
- summaries (dict of functions) – Summary functions to pass to tf; will be evaluated for outputs of ft. Each summary must have signature summary(f_pred, f_meas). Grama includes builtin options: gr.mse, gr.rmse, gr.rel_mse, gr.rsq, gr.ndme
- k (int) – Number of folds; k=5 to k=10 recommended [1]
- shuffle (bool) – Shuffle the data before CV? True recommended [1]
Notes
- Many grama functions support partial evaluation; this allows one to specify things like hyperparameters in fitting functions without providing data and executing the fit. You can take advantage of this functionality to easly do hyperparameter studies.
Returns: - Aggregated results within each of k-folds using given model and
- summary transform
Return type: DataFrame References
[1] James, Witten, Hastie, and Tibshirani, “An introduction to statistical learning” (2017), Chapter 5. Resampling Methods
Examples:
import grama as gr from grama.data import df_stang df_kfolds = ( df_stang >> gr.tf_kfolds( k=5, ft=gr.ft_rf(out=["thick"], var=["E", "mu"]), ) )
-
grama.tran_tools.tran_md¶ Model as transform
Use a model to transform data; useful when pre-processing data to evaluate a model.
Parameters: - df (DataFrame) – Data to merge
- md (gr.Model) – Model to use as transform
Returns: Output of evaluated model
Return type: DataFrame
Examples:
import grama as gr from grama.models import make_cantilever_beam md_beam = make_cantilever_beam() ## Use support points to generate a smaller---but representative---sample df_res = ( md_beam >> gr.ev_sample(n=1e3, df_det="nom", skip=True, seed=101) >> gr.tf_sp(n=100) >> gr.tf_md(md=md_beam) )
Module contents¶
-
grama.choice(a, size=None, replace=True, p=None)¶ Generates a random sample from a given 1-D array
New in version 1.7.0.
Note
New code should use the
choicemethod of adefault_rng()instance instead; please see the random-quick-start.Parameters: - a (1-D array-like or int) – If an ndarray, a random sample is generated from its elements.
If an int, the random sample is generated as if it were
np.arange(a) - size (int or tuple of ints, optional) – Output shape. If the given shape is, e.g.,
(m, n, k), thenm * n * ksamples are drawn. Default is None, in which case a single value is returned. - replace (boolean, optional) – Whether the sample is with or without replacement. Default is True,
meaning that a value of
acan be selected multiple times. - p (1-D array-like, optional) – The probabilities associated with each entry in a.
If not given, the sample assumes a uniform distribution over all
entries in
a.
Returns: samples – The generated random samples
Return type: single item or ndarray
Raises: ValueError– If a is an int and less than zero, if a or p are not 1-dimensional, if a is an array-like of size 0, if p is not a vector of probabilities, if a and p have different lengths, or if replace=False and the sample size is greater than the population sizeSee also
randint(),shuffle(),permutation()Generator.choice()- which should be used in new code
Notes
Setting user-specified probabilities through
puses a more general but less efficient sampler than the default. The general sampler produces a different sample than the optimized sampler even if each element ofpis 1 / len(a).Sampling random rows from a 2-D array is not possible with this function, but is possible with Generator.choice through its
axiskeyword.Examples
Generate a uniform random sample from np.arange(5) of size 3:
>>> np.random.choice(5, 3) array([0, 3, 4]) # random >>> #This is equivalent to np.random.randint(0,5,3)
Generate a non-uniform random sample from np.arange(5) of size 3:
>>> np.random.choice(5, 3, p=[0.1, 0, 0.3, 0.6, 0]) array([3, 3, 0]) # random
Generate a uniform random sample from np.arange(5) of size 3 without replacement:
>>> np.random.choice(5, 3, replace=False) array([3,1,0]) # random >>> #This is equivalent to np.random.permutation(np.arange(5))[:3]
Generate a non-uniform random sample from np.arange(5) of size 3 without replacement:
>>> np.random.choice(5, 3, replace=False, p=[0.1, 0, 0.3, 0.6, 0]) array([2, 3, 0]) # random
Any of the above can be repeated with an arbitrary array-like instead of just integers. For instance:
>>> aa_milne_arr = ['pooh', 'rabbit', 'piglet', 'Christopher'] >>> np.random.choice(aa_milne_arr, 5, p=[0.5, 0.1, 0.1, 0.3]) array(['pooh', 'pooh', 'pooh', 'Christopher', 'piglet'], # random dtype='<U11')
- a (1-D array-like or int) – If an ndarray, a random sample is generated from its elements.
If an int, the random sample is generated as if it were
-
grama.multivariate_normal(mean, cov, size=None, check_valid='warn', tol=1e-8)¶ Draw random samples from a multivariate normal distribution.
The multivariate normal, multinormal or Gaussian distribution is a generalization of the one-dimensional normal distribution to higher dimensions. Such a distribution is specified by its mean and covariance matrix. These parameters are analogous to the mean (average or “center”) and variance (standard deviation, or “width,” squared) of the one-dimensional normal distribution.
Note
New code should use the
multivariate_normalmethod of adefault_rng()instance instead; please see the random-quick-start.Parameters: - mean (1-D array_like, of length N) – Mean of the N-dimensional distribution.
- cov (2-D array_like, of shape (N, N)) – Covariance matrix of the distribution. It must be symmetric and positive-semidefinite for proper sampling.
- size (int or tuple of ints, optional) – Given a shape of, for example,
(m,n,k),m*n*ksamples are generated, and packed in an m-by-n-by-k arrangement. Because each sample is N-dimensional, the output shape is(m,n,k,N). If no shape is specified, a single (N-D) sample is returned. - check_valid ({ 'warn', 'raise', 'ignore' }, optional) – Behavior when the covariance matrix is not positive semidefinite.
- tol (float, optional) – Tolerance when checking the singular values in covariance matrix. cov is cast to double before the check.
Returns: out – The drawn samples, of shape size, if that was provided. If not, the shape is
(N,).In other words, each entry
out[i,j,...,:]is an N-dimensional value drawn from the distribution.Return type: ndarray
See also
Generator.multivariate_normal()- which should be used for new code.
Notes
The mean is a coordinate in N-dimensional space, which represents the location where samples are most likely to be generated. This is analogous to the peak of the bell curve for the one-dimensional or univariate normal distribution.
Covariance indicates the level to which two variables vary together. From the multivariate normal distribution, we draw N-dimensional samples,
![X = [x_1, x_2, ... x_N]](../_images/math/9391bf1d850e8ba701b49624b0ade07272831afd.png) . The covariance matrix
element
. The covariance matrix
element 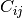 is the covariance of
is the covariance of 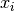 and
and 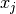 .
The element
.
The element 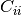 is the variance of
is the variance of 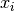 (i.e. its
“spread”).
(i.e. its
“spread”).Instead of specifying the full covariance matrix, popular approximations include:
- Spherical covariance (cov is a multiple of the identity matrix)
- Diagonal covariance (cov has non-negative elements, and only on the diagonal)
This geometrical property can be seen in two dimensions by plotting generated data-points:
>>> mean = [0, 0] >>> cov = [[1, 0], [0, 100]] # diagonal covariance
Diagonal covariance means that points are oriented along x or y-axis:
>>> import matplotlib.pyplot as plt >>> x, y = np.random.multivariate_normal(mean, cov, 5000).T >>> plt.plot(x, y, 'x') >>> plt.axis('equal') >>> plt.show()
Note that the covariance matrix must be positive semidefinite (a.k.a. nonnegative-definite). Otherwise, the behavior of this method is undefined and backwards compatibility is not guaranteed.
References
[1] Papoulis, A., “Probability, Random Variables, and Stochastic Processes,” 3rd ed., New York: McGraw-Hill, 1991. [2] Duda, R. O., Hart, P. E., and Stork, D. G., “Pattern Classification,” 2nd ed., New York: Wiley, 2001. Examples
>>> mean = (1, 2) >>> cov = [[1, 0], [0, 1]] >>> x = np.random.multivariate_normal(mean, cov, (3, 3)) >>> x.shape (3, 3, 2)
The following is probably true, given that 0.6 is roughly twice the standard deviation:
>>> list((x[0,0,:] - mean) < 0.6) [True, True] # random
-
grama.set_seed()¶ seed(self, seed=None)
Reseed a legacy MT19937 BitGenerator
Notes
This is a convenience, legacy function.
The best practice is to not reseed a BitGenerator, rather to recreate a new one. This method is here for legacy reasons. This example demonstrates best practice.
>>> from numpy.random import MT19937 >>> from numpy.random import RandomState, SeedSequence >>> rs = RandomState(MT19937(SeedSequence(123456789))) # Later, you want to restart the stream >>> rs = RandomState(MT19937(SeedSequence(987654321)))